Revisiting Pendulum Dynamics - Tap to Re-oscillate

[saltydog]

Regarding an earlier post:

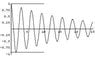
I have an underdamped pendulum. This is just what you'd expect to happen to a real pendulum if you pick it up then let it go: It slowly oscillates down to nothing. An equation describing this is:

y^{''}+0.1y^{'}+4y=0\ \ \ \ \ \ \ \ \ \ \ \ (1)

with y(0)=1 and y'(0)=0

The first plot shows this behavior: it just winds down.

However, I'd like to "tap" the pendulum at the other side just when it reaches it's maximum angular displacement and to do it with just enough force so that it comes right back to me so I can tap it again and so forth.

An equation to model this is:

y^{''}+0.1y^{'}+4y=C\delta(y-y_{max})

Where \delta(x) is the Dirac Delta function.

With C to be determined so that the pendulum comes back to the same spot.

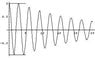
I've analyzed this for just the first half-swing and determined that c\approx1.15. That is:

y^{''}+0.1y^{'}+4y=1.15\delta(t-t1_{min})

Where I've calculated the first minimum point by solving (1) and using some trig relations. The second plot shows this result. Note at the bottom of the first valley, 1.15\delta(t-t1_{min}) is applied. Note the pendulum reaches back to 1, thus it will fall back again to where I tapped it.

Any ideas how to express this in a periodic fashion so that the once underdamped pendulum is turned into an harmonic oscillator?

 

[M98Ranger]

It is interesting to see how tapping the pendulum at just the right time and with the right amount of force can re-oscillate it and turn it into a harmonic oscillator. Your analysis and calculation of the value of C is impressive and shows a good understanding of the dynamics of the pendulum.

As for expressing this in a periodic fashion, one idea could be to use a periodic function such as a sine or cosine wave to represent the tapping force. By adjusting the amplitude and frequency of the wave, you may be able to achieve the desired effect of re-oscillating the pendulum continuously. Additionally, you could also explore using different types of forcing functions, such as a square wave or sawtooth wave, to see how they affect the behavior of the pendulum.

Overall, your approach and analysis of the pendulum dynamics is commendable and I believe with further exploration and experimentation, you can find a periodic solution to turn your underdamped pendulum into a harmonic oscillator.