Riemann Sums: Understanding Expression of Angular Coordinate Theta

[alejandrito29]

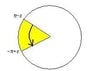
there is correct the expresion $$\int^{-\pi+\epsilon}_{\pi-\epsilon} d\theta$$...where $$\theta$$ is a angular coordinate between $$(-\pi,\pi)$$...¿what means this?...

i believe that this mean that the angular coordinate theta runs from $$\pi-\epsilon$$ to
$$-\pi+\epsilon$$ in the sense anti clock (figure)

 

[HallsofIvy]

It's a bit peculiarly written. I would use
$$\int_a^b f(x)dx= -\int_b^a f(x) dx$$
to write
$$\int_{\pi- \epsilon}^{-\pi+ \epsilon} d\theta= -\int_{-\pi+ \epsilon}^{\pi- \epsilon} d\theta$$

and it would NOT be the yellow portion of your picture but, rather, the white portion.

And, if it is really only $d\theta$ itself you are integrating,
$$\int_{\pi- \epsilon}^{-\pi+ \epsilon} d\theta= \left[ \theta\right]_{\pi- \epsilon}^{-\pi+ \epsilon}= -\pi- \epsilon- (\pi- \epsilon)= -2(\pi- \epsilon)$$
and
$$-\int_{-\pi+ \epsilon}^{\pi- \epsilon} d\theta= -\left[\theta\right]_{-\pi+ \epsilon}^{\pi- \epsilon}= -(\pi+ \epsilon-(\pi- \epsilon))= -2(\pi- \epsilon)$$
again.

 

[alejandrito29]

there is a way that the integral follows the path yelow?'...i can't to use in my problem $$\int_{-\pi}^{-\pi+\epsilon}+\int_{\pi-\epsilon}^{\pi}$$ in my problem