meulin
- 1
- 0
River bank problem! Need help urgently! :(
The water in a river flows uniformly at a constant speed of 2.50 m/s between parallel banks 80.0 m apart. You are to deliver a package directly across the river, but you can swim only at 1.50 m/s. If you choose to minimize the distance downstream that the river carries you, in what direction should you head? How far downstream would you be carried?
yf = yi + vt + (1/2)a(t^2)
xf = xi + vt + (1/2)a(t^2)
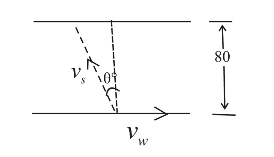
I tried to find the direction initially with this diagram from my answer key (posted below), until I realized that my answer key must be wrong because the Vs, which they indicated as the hypotenuse, is actually less than Vw, which they marked as one of the sides. I wasn't sure what to do, but I'm aware that I probably have to use derivatives in order to find it... however, I'm rather rusty at calculus as I haven't taken it in a while, so I have no idea where to start; if someone could walk me through it step by step, it would be greatly, greatly appreciated!
Thank you so much for your time and help!
P.S. Here is the picture of the diagram from my answer key:
Homework Statement
The water in a river flows uniformly at a constant speed of 2.50 m/s between parallel banks 80.0 m apart. You are to deliver a package directly across the river, but you can swim only at 1.50 m/s. If you choose to minimize the distance downstream that the river carries you, in what direction should you head? How far downstream would you be carried?
Homework Equations
yf = yi + vt + (1/2)a(t^2)
xf = xi + vt + (1/2)a(t^2)
The Attempt at a Solution
I tried to find the direction initially with this diagram from my answer key (posted below), until I realized that my answer key must be wrong because the Vs, which they indicated as the hypotenuse, is actually less than Vw, which they marked as one of the sides. I wasn't sure what to do, but I'm aware that I probably have to use derivatives in order to find it... however, I'm rather rusty at calculus as I haven't taken it in a while, so I have no idea where to start; if someone could walk me through it step by step, it would be greatly, greatly appreciated!
Thank you so much for your time and help!
P.S. Here is the picture of the diagram from my answer key: