Equanimity
- 2
- 0
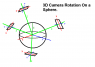
I'm using some software where the location of a plane with respect to a point is defined using spherical coordinates. I've attached a visual guide of the software parameters to this post, if someone is interested.
I'm not having problems defining the position of the plane with respect to a given origin [there are no problems calculating the polar angle theta using acos(k), the azimuthal angle phi using atan2(i, -j)* and the distance r], but I am having problems determining the rotation in the plane tangential to the sphere (positions in this plane a defined using x,y coordinates, with 0,0 being the point defined by the spherical coordinates).
Different theta/phi combinations effect a rotation in this plane. I understand why this is the case: a combination of pitch and yaw results in roll. I can observe the effect, for instance, when I open up Google Earth and rotate to a different latitude and longitude - I see that the camera rotates (the north and south directions change).
* this -j is required for the software to provide the correct answer; I believe it indicates that the plane is facing the origin of the spherical coordinate system
I'm a stuck on how to quantify this rotation. Is there a simple way to calculate the rotation in this tangential plane between two sets of i,j,k (or r, theta, phi) values?
I'm not having problems defining the position of the plane with respect to a given origin [there are no problems calculating the polar angle theta using acos(k), the azimuthal angle phi using atan2(i, -j)* and the distance r], but I am having problems determining the rotation in the plane tangential to the sphere (positions in this plane a defined using x,y coordinates, with 0,0 being the point defined by the spherical coordinates).
Different theta/phi combinations effect a rotation in this plane. I understand why this is the case: a combination of pitch and yaw results in roll. I can observe the effect, for instance, when I open up Google Earth and rotate to a different latitude and longitude - I see that the camera rotates (the north and south directions change).
* this -j is required for the software to provide the correct answer; I believe it indicates that the plane is facing the origin of the spherical coordinate system
I'm a stuck on how to quantify this rotation. Is there a simple way to calculate the rotation in this tangential plane between two sets of i,j,k (or r, theta, phi) values?