Rotation of two cylinders inclined at an angle

[PhysicsBoi1908]

Homework Statement

A cylinder P of radius r[SUB]p[/SUB] is being rotated at a constant angular velocity ω[SUB]p[/SUB] with the help of a motor about its axis that is fixed. Another cylinder Q of radius r[SUB]q[/SUB] Free to rotate about its axis that is also fixed is touched with and pressed on P making angle θ between their axes. Soon after the cylinders are pressed against each other, a steady state is reached and cylinder Q acquires a constant angular velocity. Find the final angular velocity of Q and comment on frictional force.

Relevant Equations

v= ωr

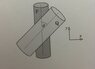
A single pair of points will be in contact between P and Q. The frictional force will try to make the velocity of these points equal.
Say the final angular velocity of Q is ω_q.

The velocity of points in contact can never be equal because of difference in directions of ω_q and ω_p. If I break ω_qr_q into horizontal and vertical components though, then I can write that its horizontal component must be equal to ω_pr_p.

Thus

ω_qr_qcosθ=ω_pr_p​

And so we get ω_q to be:

ω_q=-ω_pr_p/r_qcosθ(sinθi+cosθj)​

<br /> Which is wrong. The correct answer is:<br /> <div style="text-align: center">ω_q=-ω_pr_pcosθ/r_q(sinθi+cosθj)&#8203;</div><br /> It seems that I was supposed to break ω_pr_p into components instead. But I don&#039;t see why I should&#039;ve done that.

 

[anuttarasammyak]

As an extreme case of two cylinders are parallel position touching in line so $\theta=0$,
v=\omega_p r_p=\omega_q r_q
Another extreme case of perpendicular position, $\theta=\pi/2$,
\omega_q=0

In between
\omega_p r_p\ \cos\theta=\omega_q r_q
We get $\omega_q$ and to make it a vector
- cos\theta\ \ \mathbf{i} - sin\theta\ \ \mathbf{j}
should be multiplied.

 

[PhysicsBoi1908]

Your post is very helpful. Can you please comment if my thought process is right?
ω_p is responsible for making Q rotate. And so we take component of ω_pr_p and equate it to ω_qr_q
This is analogous to the scenario where force is applied on a box which is restricted to move along a straight line. If the force applied is inclined to the straight line, then only the component of the force along it will be responsible for the box's movement. Just like ω_pr_pcosθ is responsible for ω_qr_q

 

[anuttarasammyak]

Though not force but velocity, it seems OK.
Rotation of P with tangential speed $\omega_p r_p$ would transmit
tangential speed of Q : $\omega_p r_p \cos\theta$
longitudinal speed of Q : $\omega_p r_p \sin\theta$
So if friction allows motion of the both direction, Q rotates around and proceed along the axis.
The latter is prohibited by some mechanical arrangement and the only former survives.

 

[PhysicsBoi1908]

This is really nice. Thanks a lot!