- #1
PBear
- 5
- 0
I am having a hard time proving this to myself:
Given some object with a known inertial moment and center of mass, with r = distance from COM, do forces of equal magnitude along some line L perpendicular to R all yield the same F_t (translational force) and F_r(rotational force), and how can I prove this? How can I prove that F_t and F_r are as I have shown?
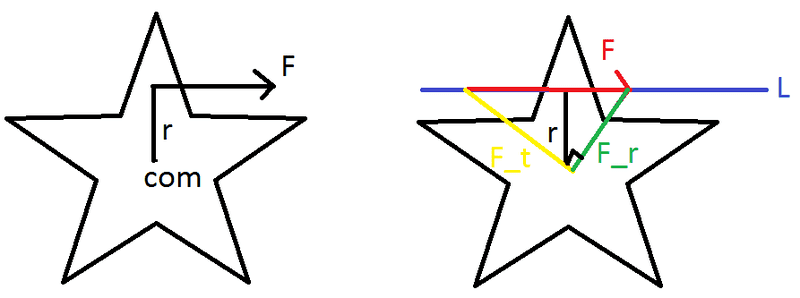
The shape shouldn't matter, only that both forces are along line L and F_t and F_r are perpendicular with F_t pointing toward the COM. I get the feeling this isn't correct because with F being applied at the point r, the F_t would be 0. If it isn't correct, how can I find the relative forces of translation and rotation acting on some free body in the way that I described?
Given some object with a known inertial moment and center of mass, with r = distance from COM, do forces of equal magnitude along some line L perpendicular to R all yield the same F_t (translational force) and F_r(rotational force), and how can I prove this? How can I prove that F_t and F_r are as I have shown?
The shape shouldn't matter, only that both forces are along line L and F_t and F_r are perpendicular with F_t pointing toward the COM. I get the feeling this isn't correct because with F being applied at the point r, the F_t would be 0. If it isn't correct, how can I find the relative forces of translation and rotation acting on some free body in the way that I described?