Rotational Dynamics / Moment of Inertia Question

[Arcarius]

Homework Statement

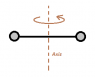
An oxygen molecule consists of two oxygen atoms whose total mass is 5.3x10^-26 kg and whose moment of inertia about an axis perpendicular to the line joining the two atoms, midway between them, is 1.9 x 10^-46 kg*m^2. From this data, estimate the effective distance between the atoms.

Homework Equations

$I = M1R^2 + M2R^2$

The Attempt at a Solution

I = (M1+M2)R^2
1.9 x 10^-46 kg*m^2 = (5.3 x 10^-26kg)R^2
R = 5.99 x 10^-11 m

Although I got that this is the radius, this is not the answer to the problem. I'm not exactly sure what I did wrong, as it seems right to me. Could anyone check my work? Thanks!

 

[TSny]

Geometrically, what do you mean by "radius" here? How does this radius relate to the distance between the atoms?

 

[Arcarius]

Geometrically, what do you mean by "radius" here. How does this radius relate to the distance between the atoms?

OH. Ugh, stupid mistake on my part! I used trig and got D to be 1.20 x 10^-10 m.
Thanks!

 

[TSny]

trig? How?

 

[Arcarius]

This is the diagram I drew, and you get that D/2 = sqrt(R^2 - I^2).
I then just solved for D, and it actually turned out to be approximately 2R.

 

[TSny]

Hmm. I imagine an oxygen molecule as being a little "dumbbell". What is "I" in your drawing?

 

[Arcarius]

Hmm. I imagine an oxygen molecule as being a little "dumbbell". What is "I" in your drawing?

I had I as the Moment of Inertia.

 

[TSny]

When you wrote the equation D/2 = sqrt(R^2 - I^2), does "I" represent moment of inertia? If so, do you see a problem with that? Note that I is not a distance, and therefore cannot be used as one side of a right triangle.

 

[Arcarius]

When you wrote the equation D/2 = sqrt(R^2 - I^2), does "I" represent moment of inertia? If so, do you see a problem with that? Note that I is not a distance, and therefore cannot be used as one side of a right triangle.

Hmm, I see what you mean. I seem to have confused the moment of Inertia with the Moment Arm. In that case, I'm not sure how to use the information I have to get an answer :/

 

[TSny]

What is the meaning of the $\small R\:$'s in the formula $\small I = m_1R_1^2 + m_2R^2$ for the moment of inertia? Would you be able to label $\small R_1$ and $\small R_2$ in the figure of the oxygen molecule that I posted earlier?

 

[Arcarius]

What is the meaning of the $\small R\:$'s in the formula $\small I = m_1R_1^2 + m_2R^2$ for the moment of inertia? Would you be able to label $\small R_1$ and $\small R_2$ in the figure of the oxygen molecule that I posted earlier?

Ohhh I see. So it is 2R, I was just lucky that the numbers worked out when I did it my way.