Nikolan
- 5
- 0
Homework Statement
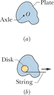
In Fig. 10-43a, an irregularly shaped plastic plate with uniform thickness and density (mass per unit volume) is to be rotated around an axle that is perpendicular to the plate face and through point O. The rotational inertia of the plate about that axle is measured with the following method. A circular disk of mass 0.500 kg and radius 2.00 cm is glued to the plate, with its center aligned with point O (Fig. 10-43b). A string is wrapped around the edge of the disk the way a string is wrapped around a top. Then the string is pulled for 5.00 s. As a result, the disk and plate are rotated by a constant force of 0.400 N that is applied by the string tangentially to the edge of the disk. The resulting angular speed is 114 rad/s. What is the rotational inertia of the plate about the axle?
Disk: m = 0.500kg
r = .002 m
Then pulled by a string for 5s resulting in 114rad/sec angular speed. This means it has 22.8 rad/sec^2 angular acceleration.
The constant force pulling the string is 0.400N.
Homework Equations
w = wo + (alpha)t
I = Icom + mh^2 (parallel axis theorem) i know this is the important equation here, but not sure how to apply it. Specifically what h would be in this equation.
Inertia equations. (not sure which other than a cylinder) Main point here is trying to find equation for rotational inertia for irregular plate.
The Attempt at a Solution
I do not know where to begin here other than what I stated in the problem statement to find angular acceleration. I'm also not sure with this question if its only asking for the rotational inertia for JUST the plate or the plate PLUS the circular disk.
Last edited: