Bolter
- 262
- 31
- Homework Statement
- Find the moment of inertia
- Relevant Equations
- PE = mgh
KE tran = 1/2mv^2
Here is the problem that I am finding difficult to answer

I had tried using conservation of energy to do this question
Where I know that the gravitational potential energy at the top of the slope equals to the sum of both the linear and rotational kinetic energy at the bottom of the slope.
Hence which is why I written down this, in where I then rearrange for I (moment of inertia). However upon doing this, I realize I have an unknown which is omega (angular velocity). How would I work out omega so I then find the moment of inertia of the ball?
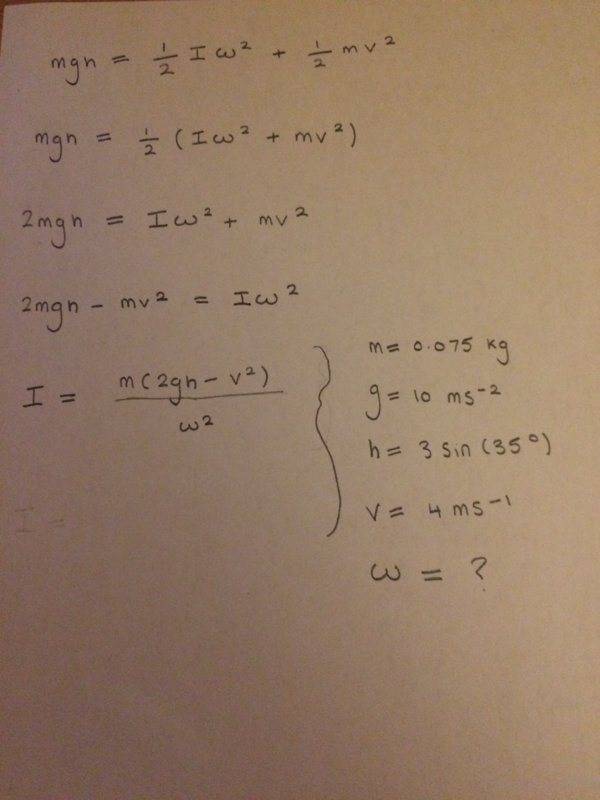
Thank you!
I had tried using conservation of energy to do this question
Where I know that the gravitational potential energy at the top of the slope equals to the sum of both the linear and rotational kinetic energy at the bottom of the slope.
Hence which is why I written down this, in where I then rearrange for I (moment of inertia). However upon doing this, I realize I have an unknown which is omega (angular velocity). How would I work out omega so I then find the moment of inertia of the ball?
Thank you!
