- #1
ILOVEPHYSIC
- 3
- 0
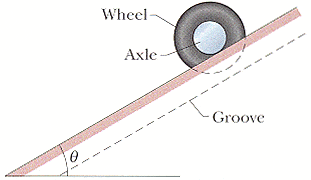
A uniform wheel of mass 14.0 kg is mounted rigidly on a massless axle through its center, as shown in the figure below. The radius of the axle is 0.200 m, and the rotational inertia of the wheel-axle combination about its central axis is 0.600 kg·m2. The wheel is initially at rest at the top of a surface that is inclined at angle θ = 30.0° with the horizontal; the axle rests on the surface while the wheel extends into a groove in the surface without touching the surface. Once released, the axle rolls down along the surface smoothly and without slipping. The wheel-axle combination moves down the surface by 3.00 m.
(a)Determine its rotational kinetic energy at this point? J
(b) Determine its translational kinetic energy at this point? J
 Mgh= 1/2mw^2 + 1/2mv^2 --(1)
Mgh= 1/2mw^2 + 1/2mv^2 --(1)
v=wR --(2)
The problem i feel confused is that what is R for since part of the wheel is inside the groove. I am not sure the question is just simply sub (2) into (1) and find the answer.
(a)Determine its rotational kinetic energy at this point? J
(b) Determine its translational kinetic energy at this point? J
v=wR --(2)
The problem i feel confused is that what is R for since part of the wheel is inside the groove. I am not sure the question is just simply sub (2) into (1) and find the answer.