WVVan
- 2
- 0
Hi All,
Thanks for your time. I'm not an engineer nor do I play one on TV. Last time I did any load calculations was in a some college M.E. classes and that was so long ago we were all still using slide rules just a couple years before. No really.
I'm going to build a fold-up table for my RV-van project ("Hal The Van"). The table is 24"x20" and attached to a cabinet by two hinges. After the table is swung into position a "U" shaped welded arrangement of three steel tubes slides out from the cabinet and supports the table from underneath. The steel tubes are supported within the cabinet by two sets of nylon bushings that allow the tubes to slide back and forth.
Hopefully this picture makes it a little clearer.
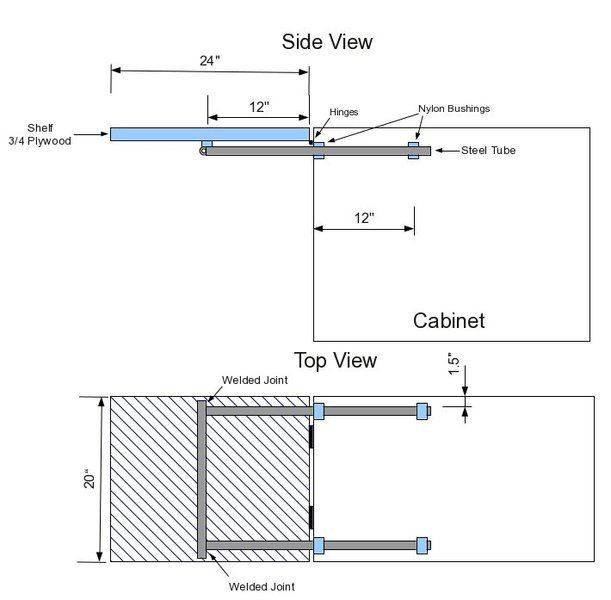
It is neither to scale nor totally accurate. Just a rough sketch.
I'd like the table to be able to support at least 50 pounds. My question is about the type/thickness of steel tube that I could use. I'm sure if I used "black iron" steel gas pipe that it would support the weight but that seems like overkill.
Instead could I use, from the http://www.mcmaster.com/" catalog page 3627,
Would this tube support the weight or would something thicker be needed?
If this tube would work what do you think (roughly) is the max load it would support?
Thanks again for your time. If this isn't clear or you have any questions please let me know.
Dave
Thanks for your time. I'm not an engineer nor do I play one on TV. Last time I did any load calculations was in a some college M.E. classes and that was so long ago we were all still using slide rules just a couple years before. No really.
I'm going to build a fold-up table for my RV-van project ("Hal The Van"). The table is 24"x20" and attached to a cabinet by two hinges. After the table is swung into position a "U" shaped welded arrangement of three steel tubes slides out from the cabinet and supports the table from underneath. The steel tubes are supported within the cabinet by two sets of nylon bushings that allow the tubes to slide back and forth.
Hopefully this picture makes it a little clearer.
It is neither to scale nor totally accurate. Just a rough sketch.
I'd like the table to be able to support at least 50 pounds. My question is about the type/thickness of steel tube that I could use. I'm sure if I used "black iron" steel gas pipe that it would support the weight but that seems like overkill.
Instead could I use, from the http://www.mcmaster.com/" catalog page 3627,
Material: General-Purpose Low-Carbon Steel
Shape: Tubes
Wall Thickness: .065"
Inside Diameter: .87"
Outside Diameter: 1"
ASTM Specification: ASTM A513
Would this tube support the weight or would something thicker be needed?
If this tube would work what do you think (roughly) is the max load it would support?
Thanks again for your time. If this isn't clear or you have any questions please let me know.
Dave
Last edited by a moderator: