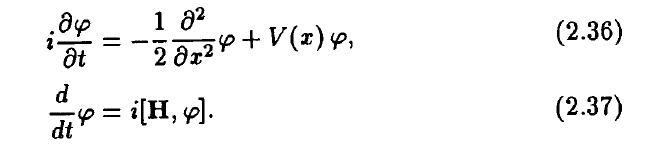SUMMARY
The discussion focuses on the derivation of the Schrödinger equation from the Heisenberg equation of motion within quantum field theory, specifically referencing Hatfield's book. Participants clarify that the Hamiltonian operator, ##\hat{H}##, is conserved in the Heisenberg picture, allowing for the evaluation of integrals at any time. The equal-time commutation relations, particularly equation (2.54), are essential for manipulating the operators involved. The correct application of these relations leads to the conclusion that the commutator of the Hamiltonian and the field operator simplifies to the form ##h \phi(x)##.
PREREQUISITES
- Understanding of quantum field theory concepts, particularly Hamiltonian operators.
- Familiarity with equal-time commutation relations in quantum mechanics.
- Knowledge of integral calculus as applied to operator algebra.
- Proficiency in manipulating differential operators, specifically the Laplacian operator.
NEXT STEPS
- Study the derivation of the Schrödinger equation from the Heisenberg equation of motion in quantum mechanics.
- Review the properties and applications of equal-time commutation relations in quantum field theory.
- Explore the implications of conserved quantities in quantum systems, focusing on Hamiltonian dynamics.
- Learn about operator algebra in quantum mechanics, including the use of commutators and their physical significance.
USEFUL FOR
Quantum physicists, graduate students in theoretical physics, and researchers focusing on quantum field theory and operator dynamics will benefit from this discussion.