pluralangel
- 4
- 1
- Homework Statement
- a projectile is launched 40° above the horizontal and lands a vertical distance of 0.943 m below and a horizontal distance of 2.4 m away; what is the initial velocity of the projectile?
- Relevant Equations
- vy = v sin θ
vx = v cos θ
v = Δd / Δt (constant velocity)
Δd = v1 Δt + 0.5a Δt^2 (uniform acceleration)
hi, so I've been trying to find the initial velocity of this projectile; but i ended up getting a negative value for seconds squared. I've gone over my solution multiple times but don't see where i went wrong. alternatively, was i supposed to take the absolute value of seconds squared?
thanks in advance for any help : )
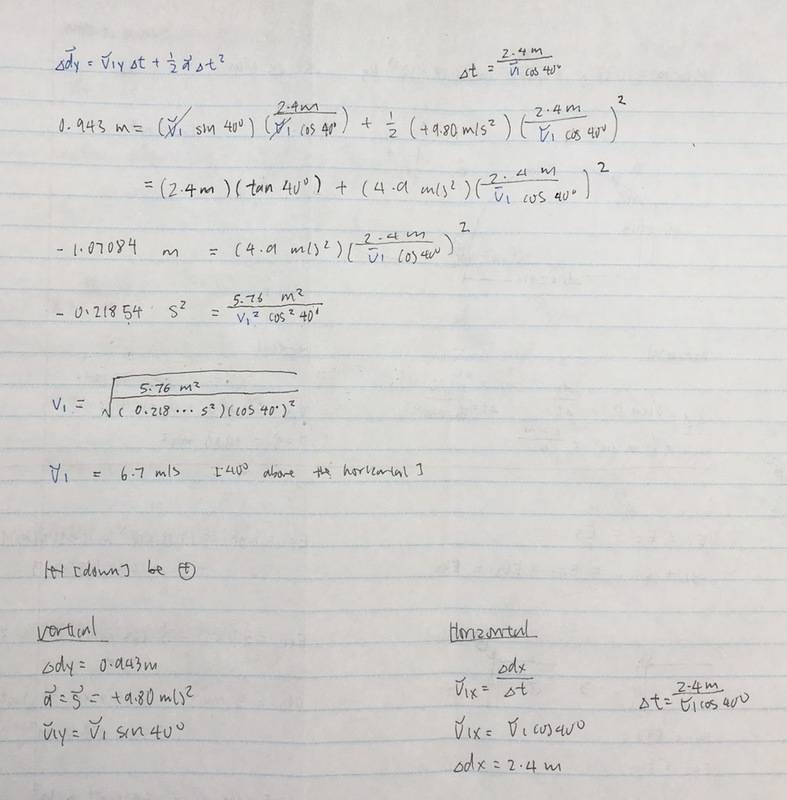
thanks in advance for any help : )