intervade
- 7
- 0
Ok it says I am to computer using a series accurate to within 0.001.
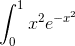
I'm really not sure where to start. Do I integrate this first by parts? Or am I thinking about this too much? Could someone point me in the right direction please! Help would be much appreciated!
I'm really not sure where to start. Do I integrate this first by parts? Or am I thinking about this too much? Could someone point me in the right direction please! Help would be much appreciated!