Series solution to 2nd order differential equation

[drsmoothe2004]

when using the power series to solve an ODE, is it always necessary to shift the index to 2 and 1 when taking the second and first derivatives of the power series respectively?

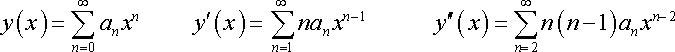
i noticed that if i don't shift the index at all and leave them at n=0, it still works out fine?

also, how will i know when to use the frobenius method vs the power series solution?

thirdly, frobenius and power series fall under the category of how to use the series solution to solve 2nd order ODEs right?

 

[CFDFEAGURU]

Hello,

I can answer the third question.

I my book "A First Course In Differential Equations" 8th Edition by Zill it is stated

The Method of Frobenius can be used to a differential equation about a regular singular point. The differential equation is to be of this form

a2(x)y''+a1(x)y'+a0(x)y=0

So yes, you are correct in stating that Frobenius can be used to find a series solution of a 2nd order ODE.

Thanks
Matt