Serway 9th ed - sliding friction and problem

[GreyNoise]

Homework Statement

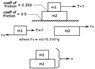
I am absolutely stumped on a problem from a trig based college physics text by Serway et. al. 8th edition. This is exercise 4.14 on page 107. The example attached to it is a 10.0 kg block M, on top of which rests a 5.0 kg block m. The coefficient of friction between the two blocks is 0.350 and the coefficient on the ground is zero (the 10.0 kg block has no friction on the ground surface). The example calculates the maximum force (tension T) that can be applied to a cable attached to the 10 kg block that will not cause the 5 kg one on top to slip. The answer is 51.5 N, and I got that part.

The exercise that follows has the same set-up, but now the cable is attached to the 5 kg block on top (see attached image), and it asks for the maximum force that can be applied to the top block without causing it to slip. The answer in the text is 27.715 N. I reasoned that the force cannot exceed the force of friction (17.5 N) between the blocks and this would pull the two blocks across the frictionless ground surface.

Homework Equations

F_s = μ_s mg

The Attempt at a Solution

Some reverse engineering got me

\frac{M+m}{M}F_s = 27.715 N

This is consistent with the answer in the text, but is it in fact the answer? How do I get there? If it is not the answer what is it? I don't even know where to start.

Regards
David C.

 

[tiny-tim]

Hi David!

i] If the tension is T, what is the acceleration, a?

ii] If the acceleration is a, what is the force on the lower block?

 

[GreyNoise]

Hello tiny-tim,

I tried, the tension on m is F_s = T = 17.15 N. So

a = \frac{17.15 N}{M}

The acceleration of M, yes? So the force on M+m is

(M+m) a = 15.0 * 1.715 \frac{kg \ast m}{s^2} = 25.72 N

Still stumped. Thnx for the help btw. I seem to have no insight into the physics of the problem yet.

 

[tiny-tim]

Hello GreyNoise!

I don't really understand what you're doing.

Assume the two blocks are moving together (without slipping).

Call the tension "T".

i] In terms of T, what is the formula for the acceleration, a, of both blocks?

ii] Using that formula for a, what is the formula for the force on the lower block?

 

[haruspex]

I reasoned that the force cannot exceed the force of friction (17.5 N) between the blocks

Just to explain why that's wrong...
That argument would work if the blocks were not accelerating. Think about the horizontal forces on the top block and apply ∑F = ma. It gives Tension - Friction = Mass * Acceleration, so the tension can exceed the frictional force without slipping.

 

[GreyNoise]

Ahh yes, I believe that the problems is seeking a formula for acceleration of both blocks in terms of the tension T whilke the cable is attached to the top block.

 

[GreyNoise]

The problem continues to vex me. The blocks are supposed to move with the same acceleration, no slipping. I calculated the acceleration on the light block m_1from

F_s = \mu N = \mu m_1g = 17.5 N

a = \mu g = 0.35*9.8 = 3.43 \frac{m}{s^2}

But I could just as easily calculate the acceleration from the heavy block m_2 by

F_s = \mu N = \mu m_1g = 17.15 N, same as above

a = \frac{\mu g }{m_2} = \frac{17.15N}{10.0kg} = 1.715 \frac{m}{s^2}, divide by m_2 which happens to equal 2m_1

Followed by (m_1+m_2) * a = 15.0 (kg) * 1.715 (m/s^2) = 25.73 N which is the correct answer. I am missing some physical insight here. Should I generally calculate the acceleration from the heavier weight in these sorts of problems? If so, how should I have known that? I am unsure of what I am missing here.

 

[haruspex]

The problem continues to vex me. The blocks are supposed to move with the same acceleration, no slipping. I calculated the acceleration on the light block m_1from

F_s = \mu N = \mu m_1g = 17.5 N

17.15

a = \mu g = 0.35*9.8 = 3.43 \frac{m}{s^2}

What is this acceleration? Static friction opposes relative motion.

I am missing some physical insight here. Should I generally calculate the acceleration from the heavier weight in these sorts of problems? If so, how should I have known that? I am unsure of what I am missing here.

The safe way, pretty much always, is to treat the blocks separately. Introduce unknowns for the forces and accelerations coupling them. Sometimes you can take a short cut by taking some blocks as a unit.
Your mistake above is in the way you calculated the acceleration of the top block. What are the forces on it?

 

[GreyNoise]

solved

Ok haruspex, how 'bout this?

(1) From the diagram, the forces acting on m_2 alone are

F_s = \mu N_1 = \mu m_1 g = 0.350*5.0*9.8 N = 17.15 N

(2) Under this force m_2 will accelerate

m_2 a = 17.15 N

a = \frac{17.15 N}{m_2} = \frac{17.15 N}{10 kg} = 1.715(\frac{m}{s^2})

(3) The blocks do NOT slip, so they accelerate together and

(m_1 + m_2)a = (5.0+10.0)*1.715 N = 25.73 N

T = 25.73 N

If my reasoning is correct then I should be able to get the same answer by picking on the smaller block m_1, and that is below

(1) From the diagram, the forces acting on m_1 alone are

T - F_s = T - \mu N_1 = T - \mu m_1 g

(2) Under this force m_1 will accelerate

m_1 a = T - \mu m_1 g

a = \frac{T - \mu m_1 g}{m_1}(\frac{m}{s^2})

(3) The blocks do NOT slip, so they accelerate together and

(m_1 + m_2)a = (m_1 + m_2)*\frac{T - \mu m_1 g}{m_1}

T = (m_1 + m_2)*\frac{T - \mu m_1 g}{m_1}

some elementary algebra leads to

T*[\frac{m_1 + m_2}{m_1} - 1] = (m_1 + m_2)*\mu g

and then substituting known values, I get

T*[\frac{5 + 10}{5} - 1] = (5 + 10)*0.350*9.8 N

T*[3 - 1] = 51.45 N

T = 51.45/2 = 25.73 N

T = 25.73 N

So obtaining the same answer gives me confidence that I am doing this correctly now. A quick check on a = (T - \mu m_1 g)/m_1 returned the same acceleration as well. Any mistakes in the above?

 

[haruspex]

Any mistakes in the above?

That all looks perfect.

 

[GreyNoise]

Thnx so much for the help haruspex! I have leaped another hurdle, so on to the rest of them now.