- #1
knowLittle
- 312
- 3
Homework Statement
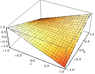
...Bounded by graphs of equations:
z=xy,
z=0,
y=x,
x=1
I don't know what z=xy is. The rest of boundaries are clear.
I assume that when y=1 and x=1, z=1. But, is this a z=1 plane?
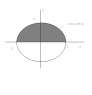
Check my figure attached.
Thank you.