Setting up a differential equation

[danielI]

So I need help with this diff eq.
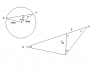
A train is placed in the tunnel AB and is will roll through it under its own weight, stop and return. Show that the time for a complete round trip is the same for all tunnels and calculate it.

Using the fact that the force of gravity (inside the earth) is proportional to the distance from the center
$$F_g = m\frac{d^2x}{dt^2} = -kx$$

I also know that $$\frac{4000}{\sin\gamma} = \frac{x}{\sin\alpha}$$ and $$\frac{F}{\sin\beta} = \frac{F_g}{\sin\alpha}$$

Is this enough? I can't delete $$\gamma$$ and $$\beta$$ which I think I should be able to.

Cheers

(the red dot is the position of the train at an arbitrary time)

 

[HallsofIvy]

Is your "$\gamma$" the angle that looks like a "v" in the picture? If so then obviously $\alpha+ \beta+ \gamma= \pi$. You can eliminate either $\beta$ or $\gamma$ but not both. You don't want to- one of them will be your variable.