Shifting of the center of mass of a system

[carlyn medona]

Homework Statement

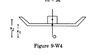
A cubical block of ice of mass m and edge L is placed in
a large tray of mass M. If the ice melts, how far does the
center of mass of the system "ice plus tray" come down ?

Homework Equations

The Attempt at a Solution

What I thought was that if no net force is acting on the system then position of center of mass should not change. But the answer in my text is mL/2(m+M). Can somebody explain me why is there a shift in center of mass.

 

[haruspex]

no net force

You are making an unwarranted assumption about the normal force on the ice from the tray.

 

[carlyn medona]

the normal force and weight is balanced right?

 

[haruspex]

the normal force and weight is balanced right?

For a mass that is not accelerating vertically that is true. But when the ice on the top melts, what happens?

 

[conscience]

For a mass that is not accelerating vertically that is true. But when the ice on the top melts, what happens?

I will not interfere with OP's attempt to find the amount by which CM shifts .

But I guess OP is having difficulty analysing the forces on melting ice . Even I am having .

On the conceptual side , I find it quite interesting that the net downward force on the ice increases as ice melts .The weight of ice/water remain same which means the Normal force on melting ice decreases . Could you explain how ?

Wouldn't the normal force , before the ice starts melting and after ice has completely melted be same ?

 

[haruspex]

I will not interfere with OP's attempt to find the amount by which CM shifts .

But I guess OP is having difficulty analysing the forces on melting ice . Even I am having .

On the conceptual side , I find it quite interesting that the net downward force on the ice increases as ice melts .The weight of ice/water remain same which means the Normal force on melting ice decreases . Could you explain how ?

Wouldn't the normal force , before the ice starts melting and after ice has completely melted be same ?

Try answering the question I posed. Consider a small piece of ice high up on one side of the block. What happens when it melts?

 

[conscience]

Try answering the question I posed. Consider a small piece of ice high up on one side of the block. What happens when it melts?

Isn't the ice in the shape of a cubical block placed at the center of the tray ?

 

[haruspex]

Isn't the ice in the shape of a cubical block placed at the center of the tray ?

Yes, but so? Does that stop your answering my question?

 

[conscience]

What happens when it melts?

Water gets dispersed on the tray . CM of the system is lowered .

Sorry , if I am not understanding your question .

 

[haruspex]

Water gets dispersed on the tray . CM of the system is lowered .

Sorry , if I am not understanding your question .

How does the melted piece reach the tray?

 

[carlyn medona]

Okay so the melted water comes down because of net downward force, which implies normal force is less than weight. So what is the net force on the system?

 

[haruspex]

Okay so the melted water comes down because of net downward force, which implies normal force is less than weight. So what is the net force on the system?

Consider the forces between the melted fragment and the solid block.

 

[carlyn medona]

So that means melted part is not in my system

 

[haruspex]

So that means melted part is not in my system

A system is whatever you define it to be. But if you define it to to be the plate, the block, and any meltwater then parts of the system can move with respect to other parts. This means you may need to analyse smaller systems to understand the forces.

 

[conscience]

How does the melted piece reach the tray?

I really don't know how to answer that question . Would you rephrase the question ?

 

[haruspex]

I really don't know how to answer that question . Would you rephrase the question ?

A fragment of the ice, high up on one side of the block, is stationary. Then it melts, and we know it ends up on the tray. By what process does it get from the top of the block to the bottom? It is a very simple question, with a very simple answer.

 

[conscience]

I agree it is a simple question but I don't have an answer . Pardon for my dumbness . Could you explain the force analysis .

 

[haruspex]

I agree it is a simple question but I don't have an answer . Pardon for my dumbness . Could you explain the force analysis .

I wasn't looking for a force analysis at this stage, just "it runs down".
The point is that it goes from stationary to moving. What does that tell you, in general terms, about the forces on it?

 

[conscience]

I wasn't looking for a force analysis at this stage, just "it runs down".
The point is that it goes from stationary to moving. What does that tell you, in general terms, about the forces on it?

That there is a net downward force on the molten ice .

 

[haruspex]

That there is a net downward force on the molten ice .

Right. So what is the affect on the normal force between the tray and the block?