- #1
emeriska
- 17
- 0
Sorry I failed to make Latex work, don't know why...
1. Homework Statement
We consider
for a given potential. Psi is also normalized...
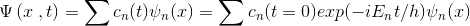
Show that expectation value of energy is independent of time.
Well, I'm use to expecting values, but not of the energy...
I started with <H>psi=<E>psi
then if I compute <H>=<psi|H|psi> = E|Psi> = E
Then I told myself H=p^2/2m + V(x)
So I guess if I compute dH/dt and I find it equals to 0 I can say E is independent of time?
I feel like this is wrong tough... It looks too simple
Thanks a lot for checking that out guys!
1. Homework Statement
We consider
for a given potential. Psi is also normalized...
Homework Equations
Show that expectation value of energy is independent of time.
The Attempt at a Solution
Well, I'm use to expecting values, but not of the energy...
I started with <H>psi=<E>psi
then if I compute <H>=<psi|H|psi> = E|Psi> = E
Then I told myself H=p^2/2m + V(x)
So I guess if I compute dH/dt and I find it equals to 0 I can say E is independent of time?
I feel like this is wrong tough... It looks too simple
Thanks a lot for checking that out guys!
Last edited: