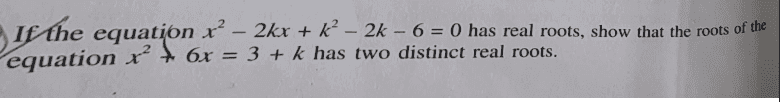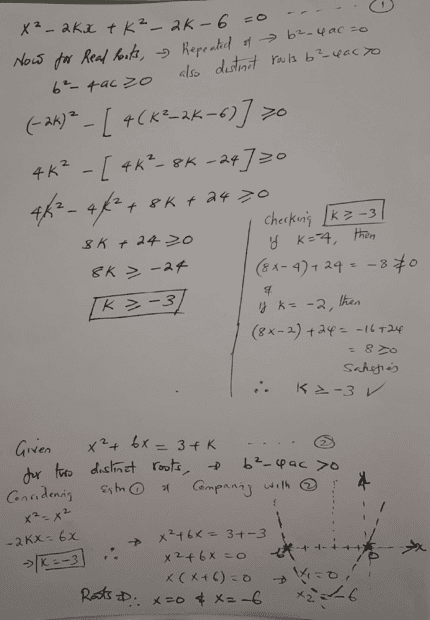SUMMARY
The discussion focuses on determining the conditions under which the quadratic equations \(x^2 + 6x = 3 + k\) and another unspecified quadratic equation have distinct real roots. The key findings indicate that for the first equation, the condition is \(k > -12\), while for the second equation, the condition is \(k \ge -3\). The analysis reveals that \(k \ge -3\) leads to two distinct roots, whereas \(k \ge -12\) results in equivalent roots. The completion of the square method is emphasized as a valid approach to derive these conditions.
PREREQUISITES
- Understanding of quadratic equations and their properties
- Familiarity with the discriminant method for determining root types
- Knowledge of the completion of the square technique
- Basic algebraic manipulation skills
NEXT STEPS
- Study the quadratic formula and its derivation
- Learn about the discriminant and its role in identifying root types
- Explore the method of completing the square in depth
- Investigate the implications of varying coefficients in quadratic equations
USEFUL FOR
Mathematics students, educators, and anyone interested in mastering quadratic equations and their properties, particularly in the context of real root analysis.