Simple circuit. Doubt with potentials

[srmico]

Hey everyone!
I'm doing this simple exercice from Halliday's book, where I have to find some intensities at some points...

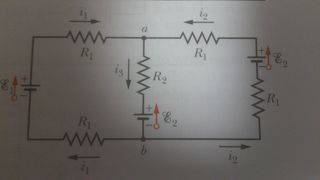
anyway after solving it, I realized that only looking at point b,and using Kirchoffs loop rule, the voltage at the negative of E1 and the voltage at the negative of E2(right) should be 0 in both points, then I get the equations:

Vb-0=i1*R1
Vb-0=i2*R1

So i1=+- i2 (the sign can be checked later).

Solving the problem the usual way, i1=2*i2 (solved in the book), which means my equations are wrong, could someone please explain why?

Thank you!

 

[BvU]

Hi Sr, welcome to PF !

What happened to the template ? Its use is mandatory in PF. It forces you to write a clear problem statement, which now is deerly missing. And to list the variables, un- and known. Give it another try, help is on the way !

 

[phinds]

And when you restate your problem using the template, explain why you think those points should be at zero volts. It may seem obvious to you, but since it's wrong, it would be helpful to us to understand why you think it's right.