Understanding Voltage in Simple Circuits: R1, R2, and R3 Explained

[waterchan]

First of all, sorry for this possibly very dumb question, but I just can't convince myself.

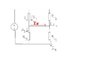
In the attached circuit diagram, I'm tempted to think that the voltage across R1 is 10V, and this would definitely be true if R1 and V were the only elements in the circuit. But doesn't the presence of R2 and R3 affect the voltage across R1 in some way, since they are both connected to the negative terminal via the same node?

R1 = 1 kiloohm, R2 = 2 kiloohms and R3 = 5.1 kiloohms, and the problem asks to find the currents across all three resistors and the voltage across R3. If the voltage across R1 isn't 10V, then I have no idea how to go about solving this problem.

Please, any advice would be appreciated.

 

[cliowa]

Dear waterchan

The voltage across R1 IS NOT 10 Volts. I don't know how much you know about electric circuits, but I suppose (considering your question) that it is (at least so far) very limited, so I'll try to explain things.

I think we can agree that there is a current going throug the circuit. This means, that there is moving electric charge. Now, let's take the battery as a starting point. The charge starts to flow, let's say in the direction towards R1. It goes through the resistor and then reaches a point, where the cable seperates. So, clearly, some of the charge will go into one wire, the other into the other wire. The amount of charge going through one of these two wires depends on the resistance it encounters (R2, R3). Finally, the charge reaches the battery.

To calculate this, you need to know some basics about circuits (idealised, as always).
First: The charge is conserved. That means that the current through the wire before it separates is exactly the same as the one after the separation. In other words: what gets into the battery comes out.
Second: The battery is the source of the voltage, which drives this circuit (it is "pushing"). The potential difference=voltage created by the battery is consumed by the circuit. So when the charge reaches the battery after one "round" there is no "pressure" left and the battery has to push it again to keep up the voltage.

The relation between the resistance (R), the current (I) and the voltage (V) has been formulated by Ohm: V=R*I. This law works fine for your purposes.

Now let's have a look at the circuit again. The resistor R1 has a given value R1=1000 Ohms, but we don't know the voltage or the current. Luckily, there's a simple way to calculate I.
Ohm's Law doesn't tell us immediately how to handle severeal resistances, so we need to construct a new circuit with only ONE resistor and a given voltage, the voltage of our battery. So we replace the resistors in your problem with just one resistor, which has the same total resistance (that's the important thing). We have to summarize the resistances in your problem.

The two most fundamental ways of having several resistors in one circuit are: serial or parallel. In your sketch resistors R2 and R3 are parallel (the current goes through them at the same time, whereby in series would mean that it goes through them in a row). The voltage across R2 and R3 is the same, as there is current coming with a certain pressure that pushes onto the two wires. One can see that the replacement resistor (Rr) for these two is given by: 1/Rr=1/R2+1/R3.

Now we have a circuit, with two resistors, R1 and Rr. These two are in series (one after the other). I earlier mentioned that the total voltage (Vtot) is consumed by the circuit, that means that Vtot= V1+Vrr, the sum of the voltages across the resistors. Applying Ohm's Law we find: Rtot*I=R1*I+Rr*I (remember that the current through the resistors is the same!). We divide by I and have: Rtot=R1+Rr.

We reached our goal: we have simplified the hole circuit to one with only one resistor. So we can calculate the current I (which is the same in both circuits), because we know the voltage (given by the battery) and the resistor (just calcuated). We are now able to go back to your problem circuit and start calculating the voltages. For example: The voltage V1 across R1 equals (Ohm's Law): V1=R1*I.

I suggest you do the rest on your own and post the results. Remember that the current splits up for passing R2 and R3. You could also derive what I just presented as a fact: that for parallel resistances the replacement resistor is given by the relation shown above.

You should also keep in mind that in the explanation i gave simplifications and assumptions have been made, most of all with Ohm's Law. As soon as your resistors start heating up for example, you really get into trouble...

Best regards...Cliowa

 

[Ouabache]

I can think of 3 ways to solve this. (depending on your level of experience).

(a) as cliowa suggested: find the total resistance in your circuit by
mathematically combining all your resistors into one. Then using Ohm's
law you can find the current thru total resistance R_tot which will be
same as the current going through R1. From there using Kirchoff's Rules
(KCL & KVL), you can find the currents and voltages in the rest of your circuit

(b) Using Nodal equations you can solve for "voltage" on the far side of R1.
(which also happens to be the voltage across R3).
Then you can easily compute the currents through R1, R3 and R3.

(c) Using Current loops you can find "currents" thru 2 paths of your
circuit. Try to choose paths that give you at most 2 unknown (currents).
You will have 2 linear equations with 2 unknowns and can solve for
both unknown currents. From there you can easily find the 3rd current using Kirchoff's rules. From there, can easily solve for the potential across R3.

I recommend using two of these methods, so you will have a way
to double check your solutions (unless you are given the solutions, then
only one method is sufficient).

Feel free to ask additional questions if you get confused. There are lots of good mentors here who can help.

 

[waterchan]

Dear Cliowa,

Thanks very much for your detailed explanation. Unfortunately, this is my very first circuits course. So from what you said, I understand that the current that flows through the combination R1 + (R2 || R3) is the same as the current flowing through R1.

Rtot = R1 + (R2 || R3) = 2437 ohms

Therefore, current through R1 = I1 = current through Rtot = (V / Rtot) = (10V / 2437ohms) = 0.0041A.

Hence, V1 = I1*R1 = (0.0041A * 1000 ohms) = 4.1 V

By Kirchoff's Voltage Law, -10V + 4.1V + V2 = 0, hence V2 = 5.9V.

Va is the voltage across R3. Since V2 and Va are in parallel, Va = V2 = 5.9V

From that point on, the current across R2 and R3 can be calculated by Ohm's Law.


Any slip-ups here?

 

[waterchan]

Thanks for the suggestions, Quabache. By methods (b) and (c), you are referring to nodal analysis and mesh analysis, am I correct? We just covered those chapters in class, and although they seem to be quicker methods, I think I'll just stick to the easy method for this one until I become skilled enough to use them.

 

[waterchan]

Current across a node?

In the attached circuit diagram, I have found the values of everything except I5 (shown with the red arrow).

Applying Kirchoff's Current Law to the intersection of R1 and R3 came to mind, but then I saw that I5 itself is on a node! If I applied KCL at this node, the equation would come out as I1 + I2 = I3 + I4 which does not do anything for I5.

Or is it valid to apply KCL at the intersection of R1 and R3, and say I1 = I3 + I5?

 

[Corneo]

Yes you can write two equations for that point.

$$I_1 -I_3 -I_5 = 0$$ and $$I_2 +I_5 -I_4 = 0$$

 

[cliowa]

Or is it valid to apply KCL at the intersection of R1 and R3, and say I1 = I3 + I5?

When thinking of applying KCL you should think of it as what it states basically, what the idea is and then see wether you can apply it.
Now, the idea is: Take some point in your circuit (can be a node, doesn't have to be) and all currents coming from one side mus proceed/ leave to the other side. All currents going in must go out, there can be no loss of current. When applying you then choose one direction as the + direction (for example leaving the point) and the other one is then the - direction. The currents then get -/+ signs and when adding them up you get zero. Of course you can rearrange things in the way proposed by Corneo.

You can easily see that Kirchhoff works well for your problem.

 

[Ouabache]

Thanks for the suggestions, Quabache. By methods (b) and (c), you are referring to nodal analysis and mesh analysis, am I correct? We just covered those chapters in class, and although they seem to be quicker methods, I think I'll just stick to the easy method for this one until I become skilled enough to use them.

Yes nodal and mesh analysis are the formal names for what I described in methods (b) and (c). Of the two, mesh analysis makes an easier cross-check for your first question. By the solutions you indicate, I don't see any slip-ups

On the 2nd question, I also would have suggested KCL equations exactly as Corneo did, which follows from the direction of currents indicated in your circuit diagram.