cyberstudent
- 7
- 0
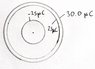
A metal sphere of radius R with a charge q is surrounded by a concentric metal sphere as shown in Figure P.23. The outer surface of the the sperical shell has a charge of + 30.0*10^-6C and the inner surface of the shell has a charge of +25.0*10^-6C.
(a) Find q
(b) Sketch qualitative graphs of (i) the radial electric field component Er and (ii) the electric potential V as functions of r.
I hired an online tutor who told me that q = -(25+30) micro coulombs
= -55 micro coulombs.
I disagree.
Shouldn't q=-25 micro coulombs? There is no electric field inside the shell, since it is a conductor. The charge residing on the outer surface of the shell therefore should not have any effect on the sphere inside the concentric shell.
Should I fire my tutor or can I have confidence in his answers?
P.S. Diagram attached
(a) Find q
(b) Sketch qualitative graphs of (i) the radial electric field component Er and (ii) the electric potential V as functions of r.
I hired an online tutor who told me that q = -(25+30) micro coulombs
= -55 micro coulombs.
I disagree.
Shouldn't q=-25 micro coulombs? There is no electric field inside the shell, since it is a conductor. The charge residing on the outer surface of the shell therefore should not have any effect on the sphere inside the concentric shell.
Should I fire my tutor or can I have confidence in his answers?
P.S. Diagram attached