randomwalk
- 1
- 0
I'm stuck on a question about deriving an expression for the magnetic susceptibility in terms of the variance of the magnetisation for a simple 2d square ising model.
I get the derivation of the specific heat, and I know am supposed to do something similar to get to the expression for susceptibility d<M>/dH. But how? Any help would be much appreciated.
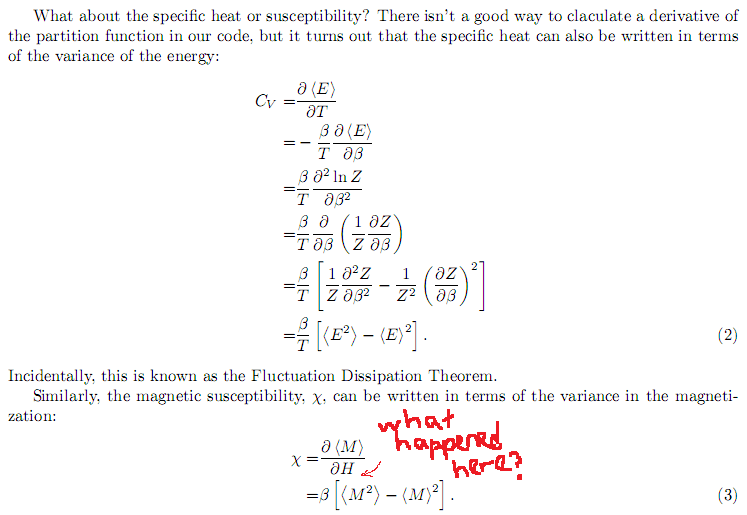
[beta is 1/KT]
I get the derivation of the specific heat, and I know am supposed to do something similar to get to the expression for susceptibility d<M>/dH. But how? Any help would be much appreciated.
[beta is 1/KT]