Ebola_V1rus
- 15
- 0
Hey all, here is a simple problem provided as a review for our final by my professor. I think I have everything right, but if history offers any insight into the future, I'm dead wrong.
Any help is greatly appreciated.
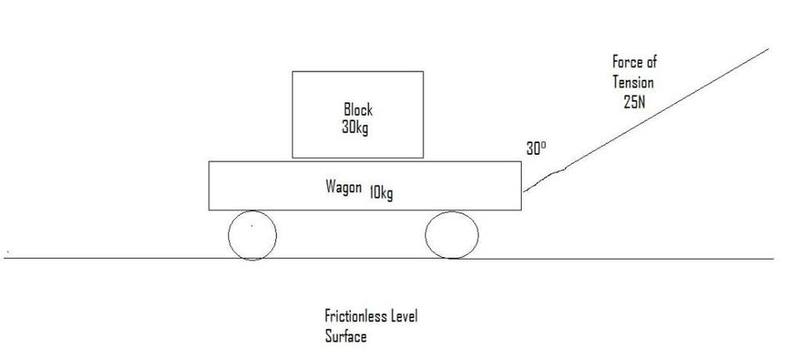
A 30kg box sits on a 10kg wagon. the wagon is pulled by a rope that is inclined at 30° above horizontal. Friction between the ground and the wagon is negligible, and the tension in the rope is 25N. The ground is level.1. Determine the magnitude of the of the frictional force acting on both the box and wagon.
2. Determine the acceleration of both the box and wagon.I've included a diagram, to make sure everyone is on the same page here.
Newton's Second Law
F = ma
Please check my logic here. We have to find the the acceleration of both the box and the wagon to determine the static friction force required to keep the box in place on top of the wagon. The +X direction is the direction in which the wagon is moving, and the +Z direction is 'UP' in the picture I included.
Since we are assuming the ground is frictionless, the only force acting on the wagon is the force of tension from the rope. So:
FnetX = sin(30°)*25N = 12.5N
We can use this answer to find the acceleration of the wagon in the +X direction.
F = ma
12.5N = 40kg(wagon + box)*a
a = .3125m/s2
Now that we know the acceleration and mass of the block, we can determine the amount of force needed from Static Friction to keep the box in place using Newton's Second Law.
FSF = 30kg * .3125m/s2 = 9.375N
So, the Frictional force acting on the block is 9.375N in the +X direction.
and the frictional force acting on the wagon is 9.375N in the -X direction.2. Determine the acceleration of both the box and wagon.
The acceleration of both the box and the wagon, as found in the previous problem, is
.3125m/s2
-Any comments or suggestions are greatly appreciated.
Any help is greatly appreciated.
Homework Statement
A 30kg box sits on a 10kg wagon. the wagon is pulled by a rope that is inclined at 30° above horizontal. Friction between the ground and the wagon is negligible, and the tension in the rope is 25N. The ground is level.1. Determine the magnitude of the of the frictional force acting on both the box and wagon.
2. Determine the acceleration of both the box and wagon.I've included a diagram, to make sure everyone is on the same page here.
Homework Equations
Newton's Second Law
F = ma
The Attempt at a Solution
1. Determine the magnitude of the of the frictional force acting on both the box and wagon.Please check my logic here. We have to find the the acceleration of both the box and the wagon to determine the static friction force required to keep the box in place on top of the wagon. The +X direction is the direction in which the wagon is moving, and the +Z direction is 'UP' in the picture I included.
Since we are assuming the ground is frictionless, the only force acting on the wagon is the force of tension from the rope. So:
FnetX = sin(30°)*25N = 12.5N
We can use this answer to find the acceleration of the wagon in the +X direction.
F = ma
12.5N = 40kg(wagon + box)*a
a = .3125m/s2
Now that we know the acceleration and mass of the block, we can determine the amount of force needed from Static Friction to keep the box in place using Newton's Second Law.
FSF = 30kg * .3125m/s2 = 9.375N
So, the Frictional force acting on the block is 9.375N in the +X direction.
and the frictional force acting on the wagon is 9.375N in the -X direction.2. Determine the acceleration of both the box and wagon.
The acceleration of both the box and the wagon, as found in the previous problem, is
.3125m/s2
-Any comments or suggestions are greatly appreciated.
