Sin(alpha)?What are the Simplified Forces at Point O?

  • Thread starter Thread starter mm391
  • Start date Start date
  • Tags Tags
    Forces Point
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
2 replies · 2K views
mm391
Messages
65
Reaction score
0

Homework Statement



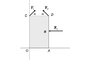
Reduce the system of forces in the diagram at point O. We know that F1 =F2 = 2F^(1/2), F =2F,and alpha =Pi/4. OA=AB=BD=a.

Homework Equations



Pythagoras
Trig Functions
F = Fxi + Fyj + Fzk
The magnitude of force F is:
F= (F2+F2+F2)^(1/2)
R=(ƩF)i+(ƩF)j+(ƩF)k
|MO| =|r|×|F|sinα

The Attempt at a Solution



Fx1 = 2F^(1/2).Cos(alpha)?
FX2 = 2F^(1/2).Cos(alpha)?
Fx3 = 2F?

Fy1 = 2F^(1/2).Sin(alpha)?
Fy2 = 2F^(1/2).Sin(alpha)?
Fy3 = 0?

R = (Fx1+Fx2+Fx3)i + (Fy1+Fy2+Fy3)j?
 

Attachments

  • Eng 1.jpg
    Eng 1.jpg
    6.6 KB · Views: 510
Last edited:
Physics news on Phys.org


yes, now sum moments of the initial given x comp of forces about O. That value divided by the resultant sum of the x comp forces will give you the y distance of the x resultant from O. Do a similar calc for moments of the y comps about O to get the x distance of the y resultant from O. The resultant passes thru that calculated point.
 


So

R=-2Fi+(2*2^(1/2)*F^(1/2)

|R|=((16F)^2+(8F))^(1/2)