Visualizing Sine and Cosine on a Unit Circle: Accurate or Not?

AI Thread Summary
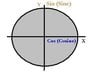
The discussion centers on the accuracy of visualizing sine and cosine on a unit circle. Participants note that the original representation lacks clarity for those unfamiliar with the concepts, as it does not explain that cosine corresponds to the x-coordinate and sine to the y-coordinate. An attached diagram is shared, which some believe provides a clearer illustration of these relationships. Overall, the conversation emphasizes the importance of effective visual representation in understanding trigonometric functions. Clear diagrams enhance comprehension for learners.
mathzeroh
Messages
98
Reaction score
0
Is this an accurate way of displaying sine and cosine on a unit circle? :wink:
 

Attachments

  • sine.JPG
    sine.JPG
    8.8 KB · Views: 592
Mathematics news on Phys.org
Well, it doesn't really contain much information, and would probably not make sense to anyone who doesn't already know that the cosine is the x coordinate of points along the unit circle and the sine is the y coordinate.

- Warren
 
See the attachment for a diagram that illustrates what I believe you were trying to say.
 

Attachments

Nice, I remember seeing that on the blackboard in my class a few years ago. :smile:
 
Zorodius said:
See the attachment for a diagram that illustrates what I believe you were trying to say.

i think that's a much better representation.
 
Thread 'Video on imaginary numbers and some queries'

Thread 'Video on imaginary numbers and some queries'

Hi, I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance! Question 1: Around 4:22, the video says the following. So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
View full post »

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »
Thread 'Unit Circle Double Angle Derivations'

Thread 'Unit Circle Double Angle Derivations'

Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
View full post »

Similar threads

B Why is sine not used for dot product?
Replies
4
Views
3K
B What are cosine and sine functions called in relation to Pi?
Replies
6
Views
2K
B Adding Sine and Cosine Waves- How to get formula
Replies
6
Views
2K
I Proving Fourier Method: Decompose Wave Forms with Sines & Cosines
Replies
1
Views
983
I Name those trigonometric functions
Replies
9
Views
2K
B Cosine or Sine of (angle+angle) always equal to 1?
Replies
4
Views
2K
Sine/cosine function and polynomial function
Replies
2
Views
2K
B Sine/Cosine behaving like a linear function
Replies
8
Views
6K
I Why is it important to convert angle units when using trigonometric functions?
Replies
8
Views
2K
I Orthogonal Basis of Periodic Functions: Beyond Sines and Cosines
3
Replies
139
Views
10K

Hot Threads

Recent Insights

Back
Top