Situation involving gravity, a quarter-circular incline plane, and friction.

[Woolverton]

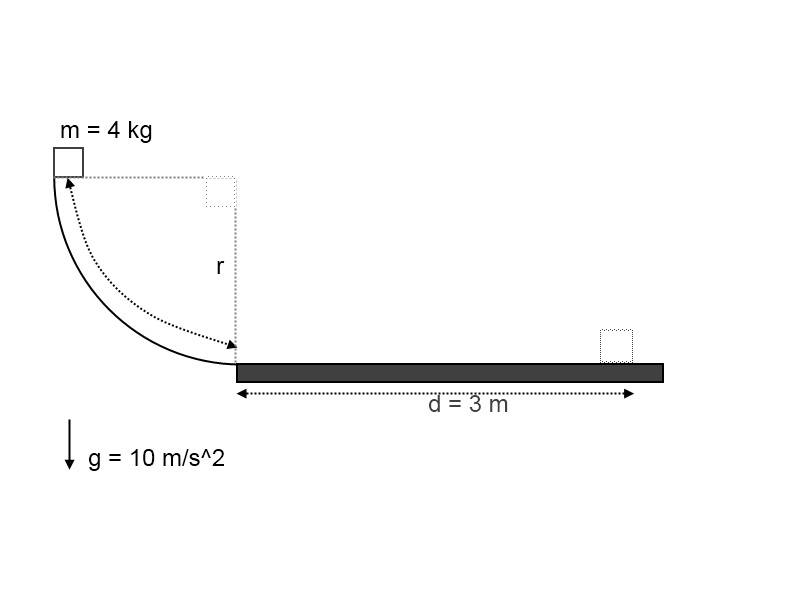
1. A block of mass 4.0 kg is released from rest at the top of a frictionless incline shaped as a quarter-circle of radius r. At the bottom of the incline, the block slides along a rough horizontal surface, experiencing frictional force of 5 N. The block comes to rest after sliding a distance of 3 meters.

(a) What is the magnitude of the block's acceleration while it slides along the rough horizontal surface?

(b) For how much time does the block slide along the rough surface before coming to rest?

(c) What is the radius of the quarter-circular incline plane?


I've drawn a sketch of the situation for your convenience. I hope it helps.

2.
g= 10 m/s²
F= m/a
x= 1/2 * at² + v₀t + x₀


3.
(a)

m = 4 kg
F = 5 N

F = ma
a= F/m

a = 5/4 = 1.25 ms/² (I'm sure this is correct)

(b)

d = 3 m
a = 1.25 m/s²

a= = d/t²
t= (d/a)^1/2

t= (3/1.25)^1/2 (not very confident about this one)

(c)

I don't know what equation to use, but I'm sure it involves the velocity of the object as it comes off of the incline.

 

[tiny-tim]

Welcome to PF!

HI Woolverton! Welcome to PF!

(a)

m = 4 kg
F = 5 N

F = ma
a= F/m

a = 5/4 = 1.25 ms/² (I'm sure this is correct)

erm … yes, but shouldn't it be negative?

(b)

d = 3 m
a = 1.25 m/s²

a= = d/t²
t= (d/a)^1/2

t= (3/1.25)^1/2 (not very confident about this one)

try your x = at + 1/2 a t² equation again …

you seem to have lost a 2 somewhere

(c)

I don't know what equation to use, but I'm sure it involves the velocity of the object as it comes off of the incline.

use conservation of energy (to find the height)