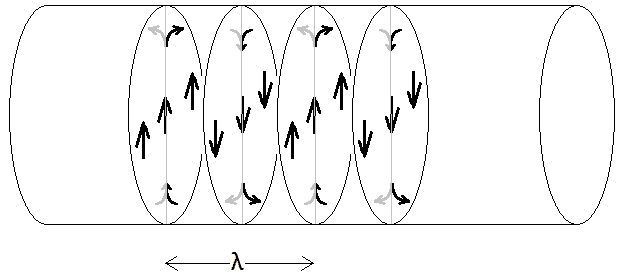
The discussion centers on the characteristics of the electric field in a linearly polarized laser beam, particularly its behavior in free space. Participants debate whether the electric field vectors bend near the beam's edges and how they form closed loops, referencing Gauss' law. There's confusion regarding the application of classical electromagnetic principles to laser beams, with some arguing that the electric field's strength diminishes toward the edges while maintaining directionality. The conversation also touches on the distinction between field lines and lines of force, and how these concepts apply to the field structure of a laser beam. Overall, the complexity of the electric field profile in a laser beam and its implications in free space remain a focal point of inquiry.