stunner5000pt
- 1,443
- 4
For the following open sets
a) |Arg z| <pi/4
b) -1 < I am z <= 1
c) (Re z)^2 > 1
Sketch the sets
Which are domains
Describe the boundary
a) |Arg z |< pi/4
well ok that means
|\theta_{0} + 2 \pi k| < \pi/4
so the theta must alwasy be less than pi/4
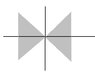
im not sure how to sketch this... i mthinking its the attached diagram, but only the triangle in the first quadrant
yes it is a domain
umm is there a way to do with without diagram??
b) -1 < I am z <= 1
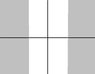
shaded part of 2
yes it is a domain
the region bounded by y = -1 from the bottom and unbounded above
c) (Re z)^2 > 1
like 3?
not a domain
unbounded
a) |Arg z| <pi/4
b) -1 < I am z <= 1
c) (Re z)^2 > 1
Sketch the sets
Which are domains
Describe the boundary
a) |Arg z |< pi/4
well ok that means
|\theta_{0} + 2 \pi k| < \pi/4
so the theta must alwasy be less than pi/4
im not sure how to sketch this... i mthinking its the attached diagram, but only the triangle in the first quadrant
yes it is a domain
umm is there a way to do with without diagram??
b) -1 < I am z <= 1
shaded part of 2
yes it is a domain
the region bounded by y = -1 from the bottom and unbounded above
c) (Re z)^2 > 1
like 3?
not a domain
unbounded