Slip Conditions for flow between Parallel Plates

[SebastianRM]

Homework Statement:

A) Analyze velocity profile
B) Determine shear stress at both walls

Relevant Equations:

Fluid flow between two parallel plates with slip of,
$$ \delta u \approx l (du/dy)$$

The problem states:

Two parallel plates separated by distance h, the plate at the top moves with velocity V, while the one at the bottom remains stationary.

My initial approach was:

I considered, $du/dy = V/h$ and for the shear stress $\tau = \mu \frac{\partial u}{\partial y}$

For $$\frac{\partial u}{\partial y} = \frac{U_{top}-U_{bottom}}{h}$$

Where I considered the fluid's velocity at the top plate to be, $U_{top} = V - \delta u$ , and at the bottom, $U_{bot} = 0 + \delta u$.

In order to improve my understanding, I searched for a diagram that illustrated the phenomena, which shows (apologies for the low quality) :

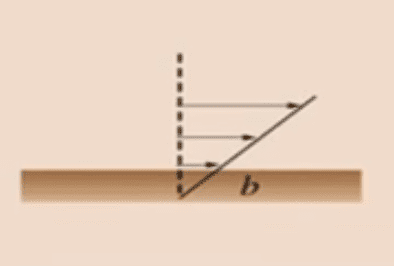
This $b$ distance in the diagram is the $l$ of my equation at the top. So I am wondering if it should be included as part of the $dy$ term, as $dy = h - l$ or should it be part of the $\partial y = h - l$ or if my original analysis was correct?

Thanks a lot guys, your time and help are very appreciated.

 

[Chestermiller]

The velocity at the top is V and the velocity at the base is 0. Forget the diagram. The shear rate is V/h.

 

[SebastianRM]

The velocity at the top is V and the velocity at the base is 0. Forget the diagram. The shear rate is V/h.

That is for no-slip condition, this is Slip condition. The velocity at the top is not V, because there is slip. Same at the bottom, the fluid is not attached to the plate, as there is slip.

 

[BvU]

Can you render the actual problem statement in full?:

 

[SebastianRM]

Can you render the actual problem statement in full?:

The diagram says *No-slip* but that is a typo (the teacher said so).

 

[BvU]

I see. In that case your picture is sensible and something similar occurs at the top plate.

Effectively $h$ is increased by $2b$. Arguing that $\tau$ is a one-side derivative is thin ice, but I suppose that's what is meant.

 

[SebastianRM]

I see. In that case your picture is sensible and something similar occurs at the top plate.

Effectively $h$ is increased by $2b$. Arguing that $\tau$ is a one-side derivative is thin ice, but I suppose that's what is meant.

I see, that makes sense. Would you say du/dy is the usual slope V/h ? While $\partial u / \partial y$ accounts for the velocity V affected by slip and the "new" height, such that $(V - 2\delta u)/(h + 2b)$ ?

 

[BvU]

Not both.

 

[Chestermiller]

I get a fluid velocity at y = 0 of $u(0)=l\gamma$, where $\gamma$ is the shear rate. And, at y = h, I get a fluid velocity of $u(h)=V-l\gamma$. So, for the shear rate, I get $$\gamma=\frac{u(h)-u(0)}{h}=\frac{(V-l\gamma)-l\gamma}{h}=\frac{V-2l\gamma}{h}$$Solving for $\gamma$ gives:$$\gamma=\frac{V/h}{\left(1+2\frac{l}{h}\right)}$$
What do you guys think?

 

[SebastianRM]

I get a fluid velocity at y = 0 of $u(0)=l\gamma$, where $\gamma$ is the shear rate. And, at y = h, I get a fluid velocity of $u(h)=V-l\gamma$. So, for the shear rate, I get $$\gamma=\frac{u(h)-u(0)}{h}=\frac{(V-l\gamma)-l\gamma}{h}=\frac{V-2l\gamma}{h}$$Solving for $\gamma$ gives:$$\gamma=\frac{V/h}{\left(1+2\frac{l}{h}\right)}$$
What do you guys think?

That is correct Sir, I think. By doing $\delta u = \ell du/dy = \ell V/(h+2l)$ we can arrive to the same form.
Thank you!