Slip & Non-Slip conditions for a Cylinder

[Trenthan]

Ey guys, this is a problem from my Mech Eng Dynamcis of Machine class

I believe i have the solution already since I've spoken to the lecture'r/tutors who run the subject but would like further clarification just incase I've done something completely wrong.

This is the problem

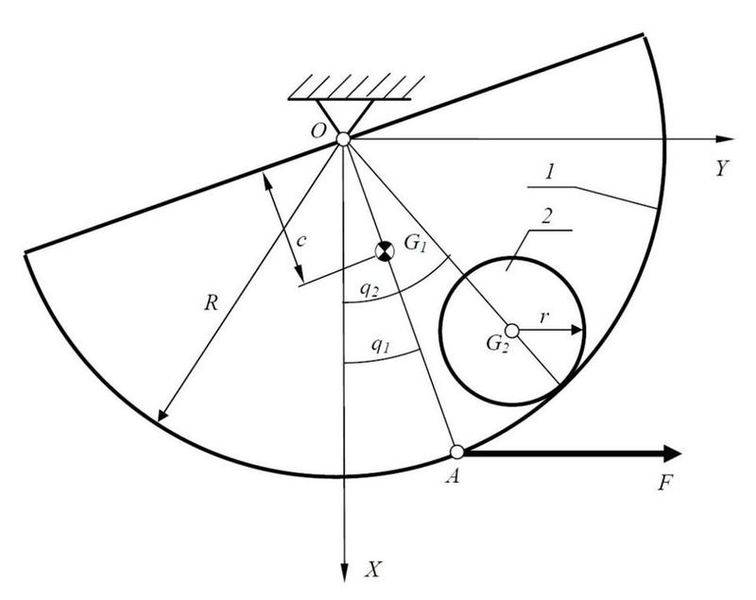
The semi cylindrical shell 1 is free to rotate about the horizontal axis Z of the inertial
system of coordinates XYZ. Its mass is M and its mass moment of inertia about the axis Z
is I1. The distance c locates its centre of gravity G1. The instantaneous position of the
shell is defined by the independent generalised coordinate q1. The cylinder 2 can roll over
the cylindrical shell without slipping. Mass of the cylinder is m and the mass moment of

inertia about its axis of symmetry is I2. The instantaneous position of the cylinder is
defined by the independent generalised coordinate q2. There is a constant and horizontal
force F applied to the shell at the point A.

a) the expression for the kinetic energy function of the system



I can easily do this, well generally can. However the slipe part is where I am struggling.


Basics first, SIMPLE case where the shell does NOT MOVE

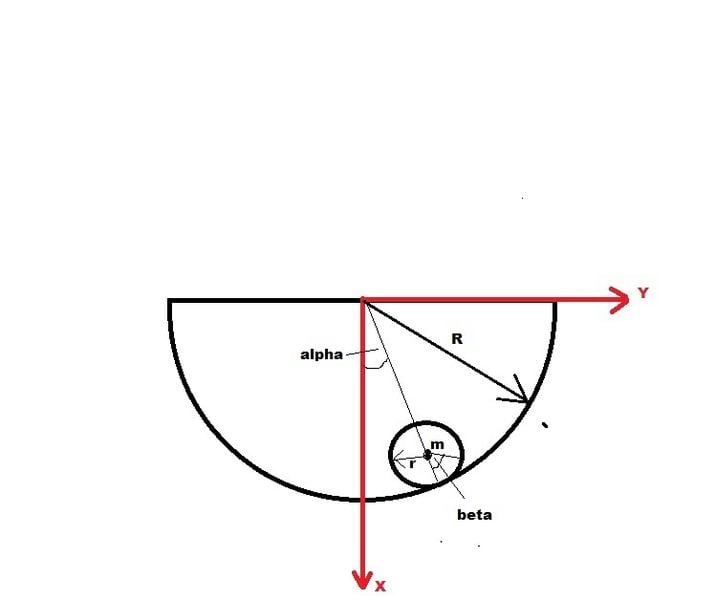
<br /> \beta r = \alpha R<br />
<br /> \beta = \alpha \frac{R}{r}<br />
<br /> \dot{\beta} = \dot{\alpha} \frac{R}{r}<br />

Now we have the above relation between angular velocity of the cylinder and its centre of mass with respect to the stationary shell.

Now here is where it gets weird for me
From what i understood, the absolut velocity of the cylinder is
<br /> \omega= \dot{\beta} - \dot{\alpha}<br />

Now when talking with the lecture'r he said you can think of it as
"the distance the cylinder rolls, minus curvature..., this is because the distance a cylinder rolls on a flat surface is a different length to the amount it does in an arc"

I understand the logic here, just not the above relation! If anyone can shed some light of where it comes from... please and thanks



Now jumping back to the main question
Using the same logic, and after speaking with him again

<br /> \beta r = (q_{2}-q_{1}) R<br />
<br /> \beta = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r}<br />


Taking into account Curvature again, gives absolute angular velocity
<br /> \omega = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r} - \dot{q_{2}} <br />


Now this i simply sub in as w in my kinetic energy equation

<br /> T_{2} = \frac{1}{2} m r_{G2}^{2} + \frac{1}{2} \omega I \omega<br />

(G2 is the Centre of Mass of the cylinder, & T₂ is the kinetic energy of the cylinder, NOT the system**)


Im not sure what I've done in the last bit is correct. Seems very iffy to me.

-The " minus curvature" and also the "q₂ - q₁ i don't like.

The "q₂ - q₁" looks to me like I am only considering the cylinder rolls the angle between the COM of the cylinder and the COM of the shell

After speaking with the tutor he did say there will be a relative component. I am not sure what i used is right though...

Any ideas guys?

Any help is appreciated guys, even if its to clarify what i have done. Or tell me the whole thnig is wrong and help point me in the right direction.

Cheers Trent, and thanks in advance

 

[hikaru1221]

I'm quite confused with your tutor's reasoning for the 1st case, so let me put it my way. See the attached picture. M is a point on the cylinder which is at the bottom of the cylinder when the cylinder is at the lowest position (or equilibrium position). The aim is to find how much the cylinder rotates about G from the equilibrium position to the position shown, which is represented by the angle gamma. From the geometrical condition: \gamma = \beta - \alpha.

As gamma shows how much the cylinder rotates about G (or in the reference frame of G), \dot{\gamma} = \dot{\beta} - \dot{\alpha} shows the angular velocity of the cylinder about G (or in the reference frame of G), which is your "absolute velocity". Only when it is angular velocity in the reference frame of G can it be applied to the formula: T = mv_G^2/2 + I\omega_G^2/2.

A more straightforward way to find that angular velocity is to consider the velocity of C, the point of contact on the cylinder. Because the cylinder rolls without slipping: \vec{v}_C=0.
Therefore: \vec{v}_G + \vec{v}_{C/G}=0
But we have: v_G = \dot{\alpha}(R-r) and \omega = v_{C/G}/r
Thus: \omega = \dot{\alpha}(R-r)/r = \dot{\beta} - \dot{\alpha}

Applying either one of those 2 methods, you can yield the same result as you did for the 2nd case

 

[Trenthan]

Thanks for the reply, i actually like your explanation far better

Only thing now is I am unsure about is incorporating the rotating the shell.


Looking at the angular velocity of the cylinder, i would have said simply replace
<br /> \dot{\alpha} = \dot{q_{2}}<br />

however the motion of the shell, will effect the angular velocity of G₂... how do we take into into account..?

same as before... (q₂ - q₁)??



Cheers Trent,

 

[hikaru1221]

Thanks for the reply, i actually like your explanation far better

Only thing now is I am unsure about is incorporating the rotating the shell.


Looking at the angular velocity of the cylinder, i would have said simply replace
<br /> \dot{\alpha} = \dot{q_{2}}<br />

I wouldn't call it so. I would rather call it "angular velocity of G₂ about center O".

however the motion of the shell, will effect the angular velocity of G₂... how do we take into into account..?

same as before... (q₂ - q₁)??

If you call it my way, you will see it obviously does NOT contain \dot{q_1}. However that doesn't mean it is not affected by the motion of the shell. In fact, the effect is already included in \dot{q_2}. But you don't even have to care about that complicated thing. Simply look at the diagram and you can be confident saying that the position of G₂ is represented by q₂ and therefore its angular velocity is \dot{q_2}.

About the angular velocity of the cylinder in the reference frame of G₂ (or about G₂), I don't quite get your tutor's explanation, so I cannot explain it in his way. If you feel comfortable with my methods, try them out