- #1
- 8,855
- 632
This needed a separate thread.
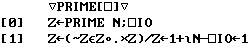
The []IO<-0 sets the "index origin" to zero so a list of numbers and indexing starts with 0 instead of 1, adding this to N has no effect, but it allows the classic 1 line approach so popular in APL programs.
It creates a list of N numbers, 2 -> N-1, (Z <- 2 + ι N). Then it creates a N by N matrix of remainders (Z ∘.| Z) for every number in the list divided by every number in the list. (Note in APL the remainder operator is residue(s) = divisor(s) | dividend(s)). It then compares 0 ≠ to that matrix of remainders to generate a matrix of boolean ones and zeros, with ones corresponding to non-zero remainders. It then creates another matrix boolean ones and zeros for every number in the list compared to every number in the list (Z ∘.= Z), which creates a zero matrix with a diagonal of 1's where the numbers are the same, which would correspond to the cases where the remainders from the first matirx would be zero, but only because the numbers were divided by themselves. Then the two boolean matrices are or'ed, resuting in a boolean matrix of ones and zeros where the ones correspond to remainders not equal to zero or numbers equal to themselves. The columns of this matrix are then and'ed vertically to produce a list of ones and zeros that correspond to primes and non-primes in the list of numbers (Z). Then this list of ones and zeroes is used to "reduce" Z so that only prime numbers are copied back into Z, which is the output from the prime function.
where the list function calls the prime function as a qualifier and/or modifier for each number it finds. List would be returning a pointer to a list that would have to be freed later though. C++ templates, being code fragments implemented as macros instead of functions, might be able to do this beter.
Here is an APL example where it's all done with no interation using N by N matrices in the intermediate propagation of data. Note, code flow in APL statements is right to left.Kajahtava said:prime number example
The []IO<-0 sets the "index origin" to zero so a list of numbers and indexing starts with 0 instead of 1, adding this to N has no effect, but it allows the classic 1 line approach so popular in APL programs.
It creates a list of N numbers, 2 -> N-1, (Z <- 2 + ι N). Then it creates a N by N matrix of remainders (Z ∘.| Z) for every number in the list divided by every number in the list. (Note in APL the remainder operator is residue(s) = divisor(s) | dividend(s)). It then compares 0 ≠ to that matrix of remainders to generate a matrix of boolean ones and zeros, with ones corresponding to non-zero remainders. It then creates another matrix boolean ones and zeros for every number in the list compared to every number in the list (Z ∘.= Z), which creates a zero matrix with a diagonal of 1's where the numbers are the same, which would correspond to the cases where the remainders from the first matirx would be zero, but only because the numbers were divided by themselves. Then the two boolean matrices are or'ed, resuting in a boolean matrix of ones and zeros where the ones correspond to remainders not equal to zero or numbers equal to themselves. The columns of this matrix are then and'ed vertically to produce a list of ones and zeros that correspond to primes and non-primes in the list of numbers (Z). Then this list of ones and zeroes is used to "reduce" Z so that only prime numbers are copied back into Z, which is the output from the prime function.
In C, pointers to functions can be passed as arguments. I often use pointer to functions to handle end actions from common code sequences, such as interrupt handlers in device drivers.Kajahtava said:In C or Java, functions cannot take functions as argument
Something similar could be impemented in C by usingCode:filter(list(2,n),prime?)
Code:
void *list(int, int, boolean (* function)(int));
void boolean prime(int);
...
list(2, n, prime);where the list function calls the prime function as a qualifier and/or modifier for each number it finds. List would be returning a pointer to a list that would have to be freed later though. C++ templates, being code fragments implemented as macros instead of functions, might be able to do this beter.
This one I don't understand. Where are m, n, and x declared to be integers, where is it implied that x is to be incremented by 1, and where is the list of all the m's being kept? For the "n % m > 0" part, is m a list of numbers or is this an iterative or recursive test?Next on is 'declarative programming', this is even clearer but at a significant performance cost. In declarative programming we are mainly concerned with what we want to do, and not how to do it. Simply said:Code:def prime n : 2 or n > 1 and n % m > 0 : prime m give all prime x : x < n.
Last edited: