mathkid81
- 1
- 0
Hi,
I was reading my astrophysics textbook and came across solid angles. I'm not sure I fully understand, for example there was a problem in the book that went as follows.
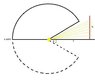
The attached "math.jpg" shows a light source (yellow) in the centre of an arc. The problem is 2D, but the arc is rotated about the x-axis to form a 3D sphere. I have the flux (F photons/sec) crossing the red line (hight h cm, zero thickness). But how do I translate that into the flux crossing the entire area after it's been rotated to be 3D.
I guess it would form a cone shape and I want the area of the face of that cone or something. So do I need to multiply the flux by the solid angle? In this case would that be 4*pi*r^2?
"math2.jpg" would represent the same problem, but just showing the cone bit. So again I have the flux crossing line of length h and zero thickness. And I want the flux that would come out of the entire cone.
I hope that makes sense. I would really appreciate any help please.
Thank you.
I was reading my astrophysics textbook and came across solid angles. I'm not sure I fully understand, for example there was a problem in the book that went as follows.
The attached "math.jpg" shows a light source (yellow) in the centre of an arc. The problem is 2D, but the arc is rotated about the x-axis to form a 3D sphere. I have the flux (F photons/sec) crossing the red line (hight h cm, zero thickness). But how do I translate that into the flux crossing the entire area after it's been rotated to be 3D.
I guess it would form a cone shape and I want the area of the face of that cone or something. So do I need to multiply the flux by the solid angle? In this case would that be 4*pi*r^2?
"math2.jpg" would represent the same problem, but just showing the cone bit. So again I have the flux crossing line of length h and zero thickness. And I want the flux that would come out of the entire cone.
I hope that makes sense. I would really appreciate any help please.
Thank you.