Solution to Gravitation Problem - Third Mass on Perpendicular Bisector

[toothpaste666]

Homework Statement

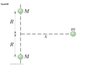
Two identical point masses, each of mass M, always remain separated by a distance of 2R. A third mass m, is then placed a distance x along the perpendicular bisector of the original two masses. (Picture attached.) Show that the gravitational force on the third mass is directed inward along the perpendicular bisector and has a magnititude of :

F = \frac{2GMmx}{(x^2+R^2)^\frac{3}{2}}

Homework Equations

F=G\frac{m1m2}{r^2}

The Attempt at a Solution

First I figured out the magnitude of the force of gravitation between one of the two mass Ms and the third mass m. To find the distance between them I used the Pythagorean theorem where:

r^2 = x^2 + R^2

plugging this and the two masses into the gravitation formula:

F = G\frac{Mm}{x^2+R^2}

That is the magnitude of the force of gravitation between each M and m. To find the magnitude and direction of the total force I should find the vector sum of these two forces? This is where I end up lost. The Pythagorean theorem won't work here. Can anyone help point me in the right direction? I know that after i find the magnitude of the resultant force I can use arctan to find the direction.

 

[SteamKing]

Hint: use vectors for the attractive force applied by each mass M on the smaller mass 'm'. Find the resultant of these two attractive forces on 'm'.

 

[Chestermiller]

You need to resolve the force into components in the x- and y directions. This will involve sines and cosines in right triangles. Geometrically, what is the cosine of the angle between the force and the bisector?

Chet

 

[toothpaste666]

You need to resolve the force into components in the x- and y directions. This will involve sines and cosines in right triangles. Geometrically, what is the cosine of the angle between the force and the bisector?

Chet

so if i take the force between one of the two Ms and m and break it into components, its y component would be:

\frac{GMmSin(theta)}{x^2+R^2}

and its x component would be:

\frac{GMmCos(theta)}{X^2+R^2}

then i do the same of the other force and add the components of the two forces so that the y components would cancel out and become 0 (same magnitude except one is above and one below the x axis) and the net x component would be \frac{2GMmCos(theta)}{X^2+R^2}

Then the resultant vector would be the radical of that squared? but that doesn't leave me with the answer I am supposed to be getting. I am still missing something =[ am I at least heading in the right direction? I am so lost lol

 

[Chestermiller]

so if i take the force between one of the two Ms and m and break it into components, its y component would be:

\frac{GMmSin(theta)}{x^2+R^2}

and its x component would be:

\frac{GMmCos(theta)}{X^2+R^2}

then i do the same of the other force and add the components of the two forces so that the y components would cancel out and become 0 (same magnitude except one is above and one below the x axis) and the net x component would be


\frac{2GMmCos(theta)}{X^2+R^2}

Then the resultant vector would be the radical of that squared? but that doesn't leave me with the answer I am supposed to be getting. I am still missing something =[ am I at least heading in the right direction? I am so lost lol

Yes. You're heading in the right direction. Now, what is cosθ in terms of the sides of a right triangle? (Hint: there was a right triangle involved when you used the Pythagorean theorem).

 

[toothpaste666]

ahh i see!

Cos(theta) = \frac{adj}{hyp} = \frac{x}{(R^2+x^2)^\frac{1}{2}}

this would make the magnitude of the force

\frac{2GMmx}{(x^2+R^2)^\frac{3}{2}}

thank you! :)

I've proved the magnitude, is showing the y components cancel out enough to prove the direction? or do i have to use arctan (y component/ x component) ?

 

[Chestermiller]

ahh i see!

Cos(theta) = \frac{adj}{hyp} = \frac{x}{(R^2+x^2)^\frac{1}{2}}

this would make the magnitude of the force

\frac{2GMmx}{(x^2+R^2)^\frac{3}{2}}

thank you! :)
I've proved the magnitude, is showing the y components cancel out enough to prove the direction?

Sure. You can see by symmetry that the y components cancel out.