Solve Calculus Problem: Find Shortest Ladder Length

[AD]

Not my own homework problem, but somebody else's.

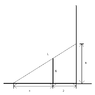
Parallel to a tall building runs a 6ft high fence. It is 2ft away from the building. What is the shortest ladder needed to reach the building from the other side of the fence?

I've drawn a diagram for this problem (see attached).

I've called the height above the ground at which the ladder touches the building 'h' and the distance of the base of the ladder from the fence 'x' and the length of the ladder 'L'.

Then

L² = h² + (x + 2)²

I think that by expressing L as a function in terms of one of the variables, x or h, and differentiating with respect to that variable, I can find then find the minimum length of the ladder.

By considering similar triangles

6/x = h/(2 + x)

So

x = 12/(h - 6)

And

h = 12/x + 6

But by substituting in either of these values, the differentiation dL/dx or dL/dh becomes horrible.

Is there an easier way to solve this problem? Am I overlooking something? I'd like to see if I could find an easier function to differentiate.

 

[arcnets]

This is the trick: Look for an extremum of L². You know that L is positive, so an extremum of L² is also an extremum of L.
I've tried
<br /> \frac{d}{dh}L^2 = 0<br />
It's lengthy but easy.

Edit: I think the rest of your work is OK.

 

[AD]

Okay, so I can do dL²/dx or dL²/dh rather than and dL/dx or dL/dh and that will make the maths easier.

You've suggested dL²/dh.

Substituting x = 12/(h - 6) into the equation for L² means that I would have to differentiate

h² + [(12/(h - 6)) + 2]²

with respect to h. Right?

 

[arcnets]

Correct.
Simplify before you derive. A lot of things will cancel.

 

[AD]

So

L² = h² + [(12/(h - 6)) + 2]²

= h² + 144/[(h - 6)²] + 48/(h - 6) + 4

What's cancelling?

 

[HallsofIvy]

Oh, c'mon. Combine the fractions before you square!

 

[AD]

To get

L² = h² + 4h²/(h - 6)²

...?

Can I simplify it further?

 

[arcnets]

I think this will do. Next, derive...

 

[AD]

How? Using the quotient rule for the second term? Is that what you did?

 

[arcnets]

Yes.