Zouatine
- 19
- 0
Homework Statement
Problem:
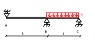
a continuous beam ABC simply presses, loaded with a distributed load q, the length of the beam is 2L.
EI=constant
find the reactions in the beam ,we use Castigiliano method.
Homework Equations
- U=(1/2EI)∫M^2 dx (U: Energy)
- dU/dP=d (d: displacement)
The Attempt at a Solution
first we have 3 reactions (Ra,Rb,Rc) in the supports.
∑F=0→ Ra+Rb+Rc=ql
∑M/A=0 → Rb+2Rc=3ql/2
for the moment flexing : 0≤x<L
- M(x)= -Ra*x .
L≤x<2L
M(x)=-Ra*x+Rb*(x-L)-(qL/2)*(x-L)^2
my problem is how to find the energy equation??
Thanx.