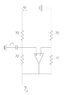
Solve e2=2/RC∫e1dt (Intregrated Circuits problem)

  • Thread starter Thread starter saravananpg
  • Start date Start date
  • Tags Tags
    Circuits
saravananpg
Messages
1
Reaction score
0
Show that the circuit of below figure has an output of e2=2/RC∫e1dt. Therefore a positive gain integrator.

Pls find the attachment for figure.

Thanks in advance for your valuable support.

Regards,
Saravanan P.G
 

Attachments

  • Drawing1-Model.jpg
    Drawing1-Model.jpg
    7.9 KB · Views: 397
Physics news on Phys.org
Hi saravananpg, welcome to PF!:smile:

As per forum policy (the rules you agreed to and should have read when you signed up for your account!), you must show some attempt at a solution to get help here.
 

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Thread 'Help to convert units of a simple formula'

The value of H equals ## 10^{3}## in natural units, According to : https://en.wikipedia.org/wiki/Natural_units, ## t \sim 10^{-21} sec = 10^{21} Hz ##, and since ## \text{GeV} \sim 10^{24} \text{Hz } ##, ## GeV \sim 10^{24} \times 10^{-21} = 10^3 ## in natural units. So is this conversion correct? Also in the above formula, can I convert H to that natural units , since it’s a constant, while keeping k in Hz ?
View full post »

Similar threads

B RC Low Pass Circuit Sine Wave Response
Replies
7
Views
3K
Purely passive RC Phase Shift Oscillator?
Replies
27
Views
3K
Resonant frequency of L - R||C circuit
Replies
21
Views
1K
RC Phase Shift Oscillator not Oscillating
Replies
41
Views
7K
Series-Parallel RC Circuit Analysis
Replies
1
Views
3K
Series-Parallel RC Circuit Analysis
Replies
2
Views
2K
Spring-mass system with a pendulum using Lagrangian dynamics
Replies
15
Views
3K
Step response of a RC circuit asking for i(t)
Replies
1
Views
2K
Finding the resonant frequency of this "discriminator" demod circuit.
Replies
2
Views
2K
Why Does Gauss' Law Yield Different Results for Spherical Charge Distributions?
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top