Aravsion
- 5
- 0
I have two problems that I have difficulty understanding and solving.
The operating efficiency of a 0.5 A, 120 V electric motor that lifts 9 kg mass agaisnt gravity at an average velocity of 0.5 m/s is most nearly what percentage?
Please help me solve this problem
2. Homework Statement
Two large, flat, parallel, conducting plates are 0.04 m apart, as shown in the picture. The lower plate is at a potential difference of 2 V with respect to ground. The upper plate is at a potential of 10 V with respect to ground. Point P is located 0.01 m above the lower plate. The electric potential at point P is? The magnitude of the electric field at point P is?
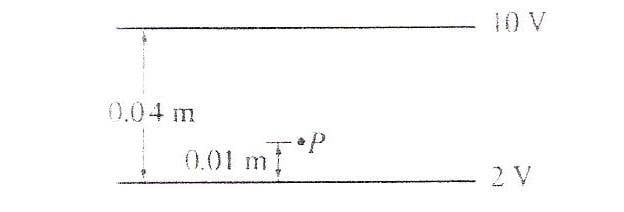
Please help me understand and solve this problem also...
Homework Statement
The operating efficiency of a 0.5 A, 120 V electric motor that lifts 9 kg mass agaisnt gravity at an average velocity of 0.5 m/s is most nearly what percentage?
Please help me solve this problem
2. Homework Statement
Two large, flat, parallel, conducting plates are 0.04 m apart, as shown in the picture. The lower plate is at a potential difference of 2 V with respect to ground. The upper plate is at a potential of 10 V with respect to ground. Point P is located 0.01 m above the lower plate. The electric potential at point P is? The magnitude of the electric field at point P is?
Please help me understand and solve this problem also...