timtng
- 25
- 0
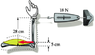
Misako wishes to measure the strength of her biceps muscle by exerting a force on a test strap. The strap is 28 cm from the pivot point at the elbow, and her biceps muscle is attached at a point 5 cm from the pivot point. If the scale reads 18 N when she exerts her maximum force, what force is exerted by the biceps muscle?
See attachment for a diagram. Please help me solve this problem.
See attachment for a diagram. Please help me solve this problem.