You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Solve Free Body Diagrams: What to Do?
- Thread starter ssj-gohan
- Start date
AI Thread Summary
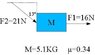
The discussion revolves around solving a free body diagram problem involving friction, specifically addressing the coefficient of friction (mu) and the forces acting on an object. Participants emphasize the need for clarity in the question, pointing out that essential details like the type of friction and the forces involved are missing. They suggest separating horizontal and vertical forces and applying Newton's Second Law to find the net force. Additionally, they note that the frictional force can be calculated using the normal force and the coefficient of friction. Ultimately, they estimate the solution to be around 15N in the right direction.
Physics news on Phys.org
Sirus
- 571
- 2
The question should really give you more information. Is mu the coefficient of static or kinetic friction? What is F_{1}? I'm assuming F_{2} is the applied force, and F_{1} is the net force. Maybe they want you to find the frictional force? Seriously, this is the worst-written question I've ever seen. Are you sure you included everthing? The way it is, there is no unknown variable. Oh boy...
bross7
- 91
- 0
What specifically are you trying to solve. The net force on the object?
If so a good place to start would be to separate your horizontal and vertical forces. Don't forget that you can convert F2 into horizontal and vertical components aswell.
Don't forget Newton's Second Law. The frictional force can be found using the normal force (all required information is given) and the coefficient of friction.
Then you should have everything you need to complete the problem and find the net force acting on the mass.
I rushed through the problem and I didn't have a calculator on hand but I believe the solution should come out to approximately 15N [R].
If so a good place to start would be to separate your horizontal and vertical forces. Don't forget that you can convert F2 into horizontal and vertical components aswell.
Don't forget Newton's Second Law. The frictional force can be found using the normal force (all required information is given) and the coefficient of friction.
Then you should have everything you need to complete the problem and find the net force acting on the mass.
I rushed through the problem and I didn't have a calculator on hand but I believe the solution should come out to approximately 15N [R].
Last edited:
In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question.
Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point?
Lets call the point which connects the string and rod as P.
Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
This problem is two parts. The first is to determine what effects are being provided by each of the elements - 1) the window panes; 2) the asphalt surface. My answer to that is
The second part of the problem is exactly why you get this affect.
And one more spoiler:
Similar threads
- Replies
- 31
- Views
- 2K
- Replies
- 4
- Views
- 990
- Replies
- 5
- Views
- 2K
- Replies
- 11
- Views
- 3K
- Replies
- 14
- Views
- 1K
- Replies
- 9
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 14
- Views
- 3K
- Replies
- 3
- Views
- 2K
- Replies
- 5
- Views
- 1K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math