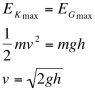Solve Jumper Question Homework: Part A & B with Initial Speed & Force

  • Thread starter Thread starter dkirov1
  • Start date Start date
AI Thread Summary
To solve the jumper question, the initial speed required to reach a height of 64 cm is calculated to be 3.5 m/s. For Part B, the force exerted by the ground during the jump can be expressed in terms of the jumper's weight, W, using the equation F = Wg, where g represents gravitational acceleration. The calculations involve determining acceleration and the time of the jump, with an estimated time of 0.117 seconds. The discussion emphasizes using energy conservation principles to relate potential and kinetic energy for a more straightforward solution. Understanding these concepts is crucial for accurately answering both parts of the homework.
dkirov1
Messages
1
Reaction score
0

Homework Statement



A person reaches a maximum height of 64 cm when jumping straight up from a crouched position. During the jump itself, the person's body from the knees up rises a distance of around 41 cm. To keep the calculations simple and yet get a reasonable result, assume that the entire body rises this much during the jump.

Part A: With what initial speed does the person leave the ground to reach a height of 64 cm?
Part B: In terms of this jumper's weight W , what force does the ground exert on him or her during the jump?

I figured out the first part, but I can't figure out the second part. :(

Also the answer to part B has to be a number? This is online homework and the answer is in the format:

F=_____W


Homework Equations



F=ma


The Attempt at a Solution


The velocity for part A was 3.5
I tried to figure out the time by using v=d/t, and got t=.117 seconds which seems wrong.
I tried to figure out the a so I used vf-vo/t=29.91?
and using 29.91 as a tried to figure it out. But I'm just stuck. I have no idea.
 
Physics news on Phys.org
The force the ground exerts on the person is going to last 41 cm, the initial velocity would be 0, the final velocity would be the answer to part a, from there you can solve for acceleration.
 
A very simple way to solve this, assuming this is a closed system, would be to use the attached formula (Egmax=Ekmax); rearrange algebraically. I would assume the force the ground exerts on her would be gravity, so F is mg or F=Wg.

Hope this helps.
 

Attachments

  • 22.png
    22.png
    3.2 KB · Views: 1,077
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

An olympic long jumper question
Replies
3
Views
1K
Force Exerted From the Ground During a Jump.
Replies
2
Views
23K
A ball is thrown w/initial speed vi at an angle 𝜃i with the horizontal
Replies
5
Views
1K
Final amplitude with damping of bungee cord
Replies
8
Views
3K
Solving for Ski Jumper Takeoff Speed: Using Energy and Motion Equations
Replies
1
Views
2K
Solving Impulse on Jumper for 50 kg Woman
Replies
9
Views
2K
What is the Ideal Angle for a Frog's Jump to Reach 3 Meters Horizontally?
Replies
19
Views
2K
Average Net force and high jumpers
Replies
27
Views
4K
Conservation of energy with a bungee jumper
Replies
8
Views
3K
Acceleration vs Time Bungee Graph
Replies
1
Views
5K

Hot Threads

Recent Insights

Back
Top