Solve Kirchhoff's Law: Find I1, I2 & I3

Thread starter sammblehh
Start date Apr 9, 2014
Tags

Law

AI Thread Summary

To solve for currents I1, I2, and I3 using Kirchhoff's laws, apply Kirchhoff's Current Law (KCL) which states that the sum of currents entering a junction equals the sum leaving, represented as I1 - I2 - I3 = 0. Additionally, use Kirchhoff's Voltage Law (KVL) which states that the sum of the electrical potential differences (voltage) around any closed network is zero, expressed as Vab + Vbc + Vcd + Vda = 0. The known values of voltage and resistance for the three resistors can be used to derive the equations needed to find the currents. By substituting the values into these equations, the currents can be calculated. Understanding and applying these laws is essential for solving circuit problems effectively.

Apr 9, 2014

sammblehh

Hi There,

Im trying to revise for a test and I need help with the following question

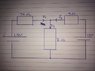
I need to find I1 I2 and I3,

I only know the voltage and resistance of the 3 resistors

I have drawn the circuit and attached it,

so stuck! please help!

Physics news on Phys.org

Apr 9, 2014

Enigman

So, what are the equations you get from Kirchoff's current law and voltage law?

Apr 9, 2014

sammblehh

i1 - i2 - i3 = 0

and

Vab + Vbc + Vcd + Vda = 0

I think

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...

View full post »

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...

View full post »

Thread 'Explain this asphalt sheen'

This problem is two parts. The first is to determine what effects are being provided by each of the elements - 1) the window panes; 2) the asphalt surface. My answer to that is The second part of the problem is exactly why you get this affect. And one more spoiler:

View full post »