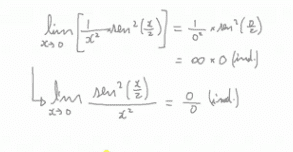Solve Math Doubt: Why Did This Happen?

[iZnoGouD]

can you explain why this happen? i can't understand

thks in advance

 

[daniel.e2718]

They're kinda the same thing...

\frac{1}{0} = \infty
\sin^2(0) = 0

so

\frac{\sin^2(0)}{0} = \underbrace{\frac{0}{0}}_\text{ind.} = \frac{1}{0}\cdot\frac{0}{1} = \underbrace{\infty\cdot0}_\text{ind.} = \frac{1}{0}\cdot\frac{\sin^2(0)}{1}

Use l'Hôpital's rule to find the value for this limit.

If \lim\limits_{x\to\alpha}\frac{f(x)}{g(x)} = \frac{0}{0} \mathrm{or} \pm\frac{\infty}{\infty}, then \lim\limits_{x\to\alpha}\frac{f(x)}{g(x)} = \lim\limits_{x\to\alpha}\frac{f'(x)}{g'(x)}

so, define functions...

f: x \ {\mapsto}\ \sin\left(\frac{1}{2} \, x\right)^{2}

g: x \ {\mapsto}\ x^{2}

Differentiate until you aren't going to get an indeterminate value (that is, make sure that the denominator does not equal zero).

\frac{\mathrm{d}g}{\mathrm{d}x} = 2 \, x

\frac{\mathrm{d}^{2}g}{\mathrm{d}x^{2}} = 2

So now the denominator will never equal zero. Differentiate f the same number of times.

\frac{\mathrm{d}f}{\mathrm{d}x} = \sin\left(\frac{1}{2} \, x\right) \cos\left(\frac{1}{2}<br /> \, x\right)

\frac{\mathrm{d}^{2}f}{\mathrm{d}x^{2}} = -\frac{1}{2} \, \sin\left(\frac{1}{2} \, x\right)^{2} +<br /> \frac{1}{2} \, \cos\left(\frac{1}{2} \, x\right)^{2}

Now divide the functions

\frac{f&#039;&#039;(x)}{g&#039;&#039;(x)} = -\frac{1}{4} \, \sin\left(\frac{1}{2} \, x\right)^{2} +<br /> \frac{1}{4} \, \cos\left(\frac{1}{2} \, x\right)^{2}

simplifies to

\frac{f&#039;&#039;(x)}{g&#039;&#039;(x)} = \frac{1}{2} \, \cos\left(\frac{1}{2} \, x\right)^{2} -<br /> \frac{1}{4}

now take the limit as x tends to zero

\lim\limits_{x\to0}\frac{1}{2} \, \cos\left(\frac{1}{2} \, x\right)^{2} -<br /> \frac{1}{4} = \frac{1}{2} \, \cos\left(0\right)^{2} -<br /> \frac{1}{4} = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}

And, to bring it all together:

\lim\limits_{x\to0}\dfrac{\sin^{2}\left(\frac{x}{2}\right)}{x^{2}} = \lim\limits_{x\to0}\frac{1}{2} \, \cos\left(\frac{1}{2} \, x\right)^{2} -<br /> \frac{1}{4} = \frac{1}{4}

I hope that helps!

 

[Levex]

I still don't understand why people want to divide by zero. It's completely nonsense...

 

[HallsofIvy]

Hey, I've never understood why people want to eat Haggis!

People continue to act irrationally!

 

[TheOtherDave]

I still don't understand why people want to divide by zero. It's completely nonsense...

It's sort of completely nearly nonsense... If the limit of whatever/x as x->0 is the same from both sides, then I call that close enough as long as it's not part of some weird "1=0" abuse of math. It is possible that I just haven't taken enough classes to know that I'm wrong, though.

 

[daniel.e2718]

Digital signal processing makes uses of poles and the \mathrm{sinc}(x) function.

The normalized \mathrm{sinc}(x) function:

<br /> \mathrm{sinc}(x) = \left\{<br /> \begin{array}{cc}<br /> 1 &amp; \text{if} \quad x = 0\\<br /> \frac{\sin(\pi \, x)}{\pi \, x} &amp; \text{if} \quad x \neq 0<br /> \end{array}<br /> \right.<br />

Has uses in DSP as its Fourier Transform is the rectangle function, which is the ideal low-pass filter.

<br /> \mathrm{rect}(\xi) = \mathcal{F}_t\left[\frac{\sin(\pi \, x)}{\pi \, x}\right]\left(\xi\right)<br />

Poles in filters determine the Q-factor, or bandwidth of the filter. I think, anyway. Or what frequencies a filter affects. I don't remember, I read some college DSP notes when high school trig was getting boring, so it went over my head a little.

<br /> \dfrac{\omega^{3} - 17 \, \omega^{2} + 94 \, \omega - 168}{\omega^{3} - 14 \, \omega^{2} + 51 \, \omega<br /> - 54} = \dfrac{{\left(\omega - 7\right)} {\left(\omega - 6\right)} {\left(\omega -<br /> 4\right)}}{{\left(\omega - 9\right)} {\left(\omega - 3\right)} {\left(\omega -<br /> 2\right)}}<br />

The above has zeros at \omega = \left[7, 6, 4\right] and poles at \omega = \left[9, 3, 2\right].

Division by zero has its uses. I'm not sure outside of DSP, though.

 

[algebrat]

You're not actually dividing by zero. You come close to dividing by zero, never do, and the ratios of the two functions that are heading to zero, that ratio may actually head towards a well-defined number.

Sorry to burst your "ooh, there's a rip in the space-time continuum" bubble.

 

[daniel.e2718]

You're not actually dividing by zero. You come close to dividing by zero, never do, and the ratios of the two functions that are heading to zero, that ratio may actually head towards a well-defined number.

Sorry to burst your "ooh, there's a rip in the space-time continuum" bubble.

This is true. But we are talking about limits, so I figured that that was implied.

 

[Whovian]

This is true. But we are talking about limits, so I figured that that was implied.

Again, there's no dividing by 0, just taking a limit. So with the greatest possible respect, shaddap. There's a lot of stuff taking limits is useful for, and if plugging in happens to result in 0/0, it's just one you can't solve by just plugging in.