Solve Mobile Pulley System: Acceleration of 3 Masses

[CAF123]

Homework Statement

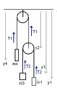
A light smooth pulley is attached to a support a fixed height above the ground. An inextensible string passes over the pulley and carries a mass 4m on one side. The other end of the string supports a similar mobile pulley; over this passes a second string, carrying masses of 3m and m on its two ends.
Deduce the acceleration of the three masses

Homework Equations

N2, Lagrange Equations

The Attempt at a Solution

I solved this already and got the correct answer using Lagrange's Equations. Now I try again with Newton's Eqns. The final set of three equations I obtain from Newtonian analysis are satisfied by the accelerations I got when I solved via Lagrange's Eqns. However, I cannot actually solve the three equations to obtain a unique solution (they are a linearly dependent set). What I need is another equation which I cannot get.
No picture was given, so I created my own and I will describe what I did.
Forces on 4m mass give eqn: T - 4mg = 4ma1, a1 the acceleration of mass 4m. This is also the tension on the other side of the same pulley. Since this pulley is the fixed pulley, it has an upward force equal to 8ma1 + 8mg

The string then passes down to the mobile pulley. Upward force on this is 4ma1 + 4mg. Consider the 3m mass: Net force is 3ma2 + 3mg and that of the m mass is ma3 + mg.
Now I used these to construct suitable equations. The net upward force on the mobile pulley is equal to the sum of the tensions 3ma2+3mg and ma3+mg. So 4ma1 + 4mg = 3ma2+3mg+mg+ma3 giving 4a1 - 3a2 -a3 = 0. (1st EQN). The tension on either side of the mobile pulley must be the same => 3ma2 + 3mg = mg + ma3 so 3a2 - a3 = -2g. (2nd EQN)

Finally, the net upward force on the fixed pulley is equal to twice the tensions on either side of the mobile pulley => 8ma1 + 8mg = 2(3ma2 + 3mg + 3ma2 + 3mg) giving 8a1 - 12a2 = 4g. (3rd EQN)

This set is linearly dependent ,so I have a free parameter
Is there another eqn I can get somewhere?

Also, now that I think about it, why is my 1st EQN valid? This pulley is mobile so its upward force need not equal the sum f two tensions below it?

Many thanks.
]

 

[arildno]

Note that the tension in the rope by which the light (massless), mobile pulley is drawn must equal twice the tension wound about it, in order for that pulley's acceleration to be finite.

Perhaps that was the equation you were lacking?

You should have 4 equations, for unknowns a_1 and T_1 (related to the fixed pulley), and a_2 and T_2 (related to the mobile pulley)

 

[CAF123]

Hi arildno,

Note that the tension in the rope by which the light (massless), mobile pulley is drawn must equal twice the tension wound about it, in order for that pulley's acceleration to be finite.

Perhaps that was the equation you were lacking?

I think I might already have taken this into account in the eqn labelled 1st EQN in the OP?
As I noted in the OP, I am not quite sure why the tension has to be twice the tension wound around it. Would this not imply the mobile pulley is in equilibrium?

 

[arildno]

Let's see:
T_1-m_1g=m_1a_1 (eq.1)

T_2-m_2g=m_2(a_1+a_2) (eq.2)

T_2-m_3g=m_3(a_1-a_2) (eq.3)
T_1=2T_2 (eq.4)

Edited away stupid g's

 

[arildno]

Hi arildno,

I think I might already have taken this into account in the eqn labelled 1st EQN in the OP?
As I noted in the OP, I am not quite sure why the tension has to be twice the tension wound around it. Would this not imply the mobile pulley is in equilibrium?

Nope. The pulley is massless (m=0), yet is subject to Newton's laws of motion.
Thus, if there is an imbalance of forces working on it, it will have infinite acceleration.

 

[arildno]

Oops, why did I put in those g-factors?

 

[arildno]

Dividing (2) and (3) with respective masses, adding them together for a_2-removal, and using (4) for T_2 removal should yield (5):
$$\frac{T_{1}}{4}\frac{m_{2}+m_{3}}{m_{2}m_{3}}-g=a_{1} (5)$$
This can then be used with (1)
EDIT:
$$\frac{T_{1}}{4}\frac{m_{2}+m_{3}}{m_{2}m_{3}}-g=-a_{1} (5)$$

 

[CAF123]

Nope. The pulley is massless (m=0), yet is subject to Newton's laws of motion.
Thus, if there is an imbalance of forces working on it, it will have infinite acceleration.

Okay, this makes sense. But I don't understand your eqns (2) and (3) yet, in particular as to why you have (a1+a2) and (a1-a2) on the right hand sides.

 

[arildno]

Hmm..I must think about this..

 

[arildno]

Okay, this makes sense. But I don't understand your eqns (2) and (3) yet, in particular as to why you have (a1+a2) and (a1-a2) on the right hand sides.

You're right, it should be (-a_1+a_2) and (-a_1-a_2)

Relative to their common acceleration -a_1, they have opposite accelerations.

 

[arildno]

Dividing (2) and (3) with respective masses, adding them together for a_2-removal, and using (4) for T_2 removal should yield (5):
$$\frac{T_{1}}{4}\frac{m_{2}+m_{3}}{m_{2}m_{3}}-g=a_{1} (5)$$
This can then be used with (1)
EDIT:
$$\frac{T_{1}}{4}\frac{m_{2}+m_{3}}{m_{2}m_{3}}-g=-a_{1} (5)$$

This is now corrected to quoted edit.

 

[arildno]

We therefore have, from (5):
$$T_{1}=\frac{4m_{2}m_{3}}{m_{2}+m_{3}}g-\frac{4m_{2}m_{3}}{m_{2}+m_{3}}a_{1}$$

 

[arildno]

We gain, by insertion:
$$\frac{4m_{2}m_{3}-m_{1}(m_{2}+m_{3})}{m_{2}+m_{3}}g=\frac{4m_{2}m_{3}+m_{1}(m_{2}+m_{3})}{m_{2}+m_{3}}a_{1}$$, that is
$$a_{1}=\frac{4m_{2}m_{3}-m_{1}(m_{2}+m_{3})}{4m_{2}m_{3}+m_{1}(m_{2}+m_{3})}g$$

 

[CAF123]

You're right, it should be (-a_1+a_2) and (-a_1-a_2)

Relative to their common acceleration -a_1, they have opposite accelerations.

Sorry what I meant was why is there two terms on the RHS. On the m2 mass, there exists a gravitational force downwards and a tension force upwards. This gives T_2 - m_2g = m_2(a_2) only, no? Similarly for the other mass: T_2 - m_3g = m_3(a_3).

If I rearrange for T_2 in the second and sub in the first, gives me a_3 - 3a_2 = 2g, which is my 2nd EQN in the OP.

 

[arildno]

"T_2 - m_2g = m_2(a_2) only, no? Similarly for the other mass: T_2 - m_3g = m_3(a_3)."

Only in the INERTIAL frame relative to the fixed pulley.

Your a_2 can be written as a_2=-a_1+a*, where a* is the relative acceleration of mass_2 to the moving pulley, which is -a_1.
Similarly, because the rope around the mobile pulley must remain fixed in length,
your a_3 can be written as a_3=-a_1-a*

 

[arildno]

Note that the terms -m_2a_1 and -m_3a_1 can be regarded as contributions from the fictitious forces in a non-inertial frame of reference.

 

[CAF123]

"T_2 - m_2g = m_2(a_2) only, no? Similarly for the other mass: T_2 - m_3g = m_3(a_3)."

Only in the INERTIAL frame relative to the fixed pulley.

Your a_2 can be written as a_2=-a_1+a*, where a* is the relative acceleration of mass_2 to the moving pulley, which is -a_1.

Should that be a* = -a_2? The acceleration of the m_2 relative to the fixed pulley (a_2F) is the (vector)sum of the acceleration of m_2 relative to the mobile pulley(a_2M) + the acceleration of the mobile pulley relative to the fixed pulley(a_MF)

a_2F = a_2, a_2M =(+/-)a_2 and I am unsure of a_MF. How did you determine the signs here?

 

[arildno]

When it comes to the sign of a_2, i.e the relative accelerations masses 2 and 3 have relative to the mobile pulley, the ONLY thing that matters is that we have OPPOSITE signs for masses 2 and 3.
This is also the case for a_1: if we call the mass 1 acceleration for a_1, the mobile pulley must have -a_1 as its acceleration.
We could have chosen oppositely, it does not matter.
--------------
The total correct sign distribution is ensured that the tensions work opposite to gravity, and that opposite accelerations have opposite signs.

 

[CAF123]

When it comes to the sign of a_2, i.e the relative accelerations masses 2 and 3 have relative to the mobile pulley, the ONLY thing that matters is that we have OPPOSITE signs for masses 2 and 3.
This is also the case for a_1: if we call the mass 1 acceleration for a_1, the mobile pulley must have -a_1 as its acceleration.
We could have chosen oppositely, it does not matter.
--------------
The total correct sign distribution is ensured that the tensions work opposite to gravity, and that opposite accelerations have opposite signs.

Just to check a couple of things: So what you did was reexpress all the accelerations of the masses relative to the fixed pulley, yes? In the equation T_2 - m_2g = m_2a_2, this is valid for the acceleration of m_2 relative to the mobile pulley?

 

[arildno]

Just to check a couple of things: So what you did was reexpress all the accelerations of the masses relative to the fixed pulley, yes? In the equation T_2 - m_2g = m_2a_2, this is valid for the acceleration of m_2 relative to the mobile pulley?

Yes to the first!

No to the second, it is not, because the moving pulley system is NON-INERTIAL.
Thus, the correct representation relative to the moving system accelerating with -a_1 is:
-(-m_2a_1)+T_2-m_2g_2=m_2a_2,
where a_2 is the acceleration of m_2 relative to the moving pulley.
The first term is the fictitious force associated with the noninertial frame's acceleration, relative to an inertial frame.

Note that THIS force law is equivalent to the one I gave.

 

[CAF123]

Okay, it was just this line which confuses me a little:

"T_2 - m_2g = m_2(a_2) only, no? Similarly for the other mass: T_2 - m_3g = m_3(a_3)."

Only in the INERTIAL frame relative to the fixed pulley.

Isn't the acceleration of a_2 relative to the fixed pulley a_2 - a_1?

 

[arildno]

$$a_{2}=\frac{1}{2}(\frac{T_{2}}{m_{2}}-\frac{T_{2}}{m_{3}})=\frac{2m_{1}(m_{3}-m_{2})}{4m_{2}m_{3}+m_{1}(m_{2}+m_{3})}g$$

The absolute acceleration a_2,abs, which is the one you gained by Lagrangian tricks of the trade, should then be:
$$a_{2,abs}=-a_{1}+a_{2,rel},a_{3,abs}=-a_{1}-a_{2,rel}$$
where I in the quoted post used a_2 for a_2,rel.

 

[arildno]

Okay, it was just this line which confuses me a little:Isn't the acceleration of a_2 relative to the fixed pulley a_2 - a_1?

In THAT line, "a_2" and "a_3" has NOT been decomposed in the common acceleration component -a_1, and the RELATIVE accelerations to the moving pulleys.

I pointed that out in the post there, I believe.

Thus, there has arisen an unfortunate confusion as to mass 2's ABSOLUTE acceleration, and mass 2's relative acceleration.

To restate, for mass 2:
We clearly have:
$$T_{2}-m_{2}g=m_{2}a_{2,abs}$$
But, that can still be written, "inertially", by setting $a_{2,abs}=-a_{1}+a_{2,rel}$
as:
$$T_{2}-m_{2}g=m_{2}(-a_{1}+a_{2,rel})$$
which, to transform it to its NON-inertial form reads:
$$-m_{2}(-a_{1})+T_{2}-m_{2}g=m_{2}a_{2,rel}$$

I hope that clears up most of your confusion, rather than adding to it.

In the post directly above this, I use $$a_{2}=a_{2,rel}$$

 

[CAF123]

I hope that clears up most of your confusion

It does, thanks. So now all I have to do is solve those 4 eqns (I understand how they were derived now).

Going back to my solution in the OP, the eqns I got there where satisfied by the solutions I got in the Lagrangian method. Why is this? I did not refer to the inertial frame of the fixed pulley, particularly when writing $T_2 - m_2g = m_2a_2$ for example.

 

[arildno]

Well, I don't remember you posted your Lagrangian version?

 

[CAF123]

Well, I don't remember you posted your Lagrangian version?

Sorry, what I mean is that the answers I got for the accelerations in the Lagrangian method satisfy the three equations I posted in the OP. So that seems to hint that those equations are correct. But I did not reference the inertial frame of the fixed pulley in my equation for mass 2: I simply wrote T-m_2g = m_2a_2, so at the moment, I don't quite understand why those equations in the OP were correct.

 

[arildno]

Well, but remember if you have a variatonal approach, say with an integrand T-V, where "T" is kinetic energy" and "V" is the potential from external forces, you should not get any tensions to solve for at all, because they are internal forces to the WHOLE system.
In such an approach, you should be able, to derive 3 equations for the three unknown velocities/accelerations, without having to bother with the intricacies of locally acting tension and finicky relative, versus absolute accelerations.
----
It's been awhile since I did this sort of thing, but variational approaches are often much simpler to work with.

 

[CAF123]

Well, but remember if you have a variatonal approach, say with an integrand 2T-V, where "T" is kinetic energy" and "V" is the potential from external forces, you should not get any tensions to solve for at all, because they are internal forces to the WHOLE system.
In such an approach, you should be able, to derive 3 equations for the three unknown velocities/accelerations, without having to bother with the intricacies of locally acting tension and finicky relative, versus absolute accelerations.
----
It's been awhile since I did this sort of thing, but variational approaches are often much simpler to work with.

Yes, in the Lagrangian method, I did not have any tensions to deal with because they are already embodied in the constraint eqns. The method I posted in the OP was not lagrangian, it was Newtonian. In my analysis there for mass 2 and 3, I did not refer to the inertial frame of the fixed pulley. Do you agree with my 3 eqns in the OP?

 

[arildno]

OKAY, let's have a look at the original:
" T - 4mg = 4ma1, a1 the acceleration of mass 4m. This is also the tension on the other side of the same pulley. Since this pulley is the fixed pulley, it has an upward force equal to 8ma1 + 8mg

The string then passes down to the mobile pulley. Upward force on this is 4ma1 + 4mg. Consider the 3m mass: Net force is 3ma2 + 3mg and that of the m mass is ma3 + mg.
Now I used these to construct suitable equations. The net upward force on the mobile pulley is equal to the sum of the tensions 3ma2+3mg and ma3+mg. So 4ma1 + 4mg = 3ma2+3mg+mg+ma3 giving 4a1 - 3a2 -a3 = 0. (1st EQN). The tension on either side of the mobile pulley must be the same => 3ma2 + 3mg = mg + ma3 so 3a2 - a3 = -2g. (2nd EQN)

Finally, the net upward force on the fixed pulley is equal to twice the tensions on either side of the mobile pulley => 8ma1 + 8mg = 2(3ma2 + 3mg + 3ma2 + 3mg) giving 8a1 - 12a2 = 4g. (3rd EQN)"
-------------------------------
1. "T - 4mg = 4ma1, a1 the acceleration of mass 4m"
Agreed!
2. "This is also the tension on the other side of the same pulley"
Agreed!
3. "Since this pulley is the fixed pulley, it has an upward force equal to 8ma1 + 8mg"
Agreed, but why bother with this static pulley at all?
4. "The string then passes down to the mobile pulley. Upward force on this is 4ma1 + 4mg."
Agreed.
5. "Consider the 3m mass: Net force is 3ma2 + 3mg"
True, this is in an inertial frame, with absolute acceleration, and your "net force" is T_2
6. "that of the m mass is ma3 + mg"
Also true, and this also equals T_2
7. "The net upward force on the mobile pulley is equal to the sum of the tensions 3ma2+3mg and ma3+mg. So 4ma1 + 4mg = 3ma2+3mg+mg+ma3 giving 4a1 - 3a2 -a3 = 0. (1st EQN)"
True.
8. "3ma2 + 3mg = mg + ma3 so 3a2 - a3 = -2g. (2nd EQN)"
True.
9. "Finally, the net upward force on the fixed pulley is equal to twice the tensions on either side of the mobile pulley => 8ma1 + 8mg = 2(3ma2 + 3mg + 3ma2 + 3mg) giving 8a1 - 12a2 = 4g. (3rd EQN)""
This is where your linear dependence arrives, it is nothing else than your first equation, where you said T_1 equals the sum of the two tensions from below.

10. What you are lacking then, is a similar eq. as in 8 for the other mass, and in addition, either the requirement that the two lower tensions must be equal to each other, or the tricky condition that the accelerations a_2 and a_3, for you absolute quantities must have a relation to each other on the requirement that the rope about mobile pulley remains of constant length.

 

[CAF123]

OKAY, let's have a look at the original:
" T - 4mg = 4ma1, a1 the acceleration of mass 4m. This is also the tension on the other side of the same pulley. Since this pulley is the fixed pulley, it has an upward force equal to 8ma1 + 8mg

The string then passes down to the mobile pulley. Upward force on this is 4ma1 + 4mg. Consider the 3m mass: Net force is 3ma2 + 3mg and that of the m mass is ma3 + mg.
Now I used these to construct suitable equations. The net upward force on the mobile pulley is equal to the sum of the tensions 3ma2+3mg and ma3+mg. So 4ma1 + 4mg = 3ma2+3mg+mg+ma3 giving 4a1 - 3a2 -a3 = 0. (1st EQN). The tension on either side of the mobile pulley must be the same => 3ma2 + 3mg = mg + ma3 so 3a2 - a3 = -2g. (2nd EQN)

Finally, the net upward force on the fixed pulley is equal to twice the tensions on either side of the mobile pulley => 8ma1 + 8mg = 2(3ma2 + 3mg + 3ma2 + 3mg) giving 8a1 - 12a2 = 4g. (3rd EQN)"
-------------------------------
1. "T - 4mg = 4ma1, a1 the acceleration of mass 4m"
Agreed!
2. "This is also the tension on the other side of the same pulley"
Agreed!
3. "Since this pulley is the fixed pulley, it has an upward force equal to 8ma1 + 8mg"
Agreed, but why bother with this static pulley at all?
4. "The string then passes down to the mobile pulley. Upward force on this is 4ma1 + 4mg."
Agreed.
5. "Consider the 3m mass: Net force is 3ma2 + 3mg"
True, this is in an inertial frame, with absolute acceleration, and your "net force" is T_2
6. "that of the m mass is ma3 + mg"
Also true, and this also equals T_2
7. "The net upward force on the mobile pulley is equal to the sum of the tensions 3ma2+3mg and ma3+mg. So 4ma1 + 4mg = 3ma2+3mg+mg+ma3 giving 4a1 - 3a2 -a3 = 0. (1st EQN)"
True.
8. "3ma2 + 3mg = mg + ma3 so 3a2 - a3 = -2g. (2nd EQN)"
True.
9. "Finally, the net upward force on the fixed pulley is equal to twice the tensions on either side of the mobile pulley => 8ma1 + 8mg = 2(3ma2 + 3mg + 3ma2 + 3mg) giving 8a1 - 12a2 = 4g. (3rd EQN)""
This is where your linear dependence arrives, it is nothing else than your first equation, where you said T_1 equals the sum of the two tensions from below.

10. What you are lacking then, is a similar eq. as in 8 for the other mass, and in addition, either the requirement that the two lower tensions must be equal to each other, or the tricky condition that the accelerations a_2 and a_3, for you absolute quantities must have a relation to each other on the requirement that the rope about mobile pulley remains of constant length.

Thanks arildno, I have to go now, but will work on it later.

 

[arildno]

Hmm..seems I specified 4 equations, rather than 3.
The kinematic relation between the two accelerations is the one that is lacking; it represents a distinct constraint requirement the rest does not provide for (and which is embedded in the Lagrangian equations of motion).

 

[CAF123]

Hmm..seems I specified 4 equations, rather than 3.
The kinematic relation between the two accelerations is the one that is lacking; it represents a distinct constraint requirement the rest does not provide for (and which is embedded in the Lagrangian equations of motion).

If we consider the mobile pulley and m2 and m3, then isn't a2 = -a3 since the string is of constant length and no slip? This turns out in the end to be incorrect, but I am not sure why

 

[Saitama]

If we consider the mobile pulley and m2 and m3, then isn't a2 = -a3 since the string is of constant length and no slip?

No, this is not correct. The accelerations are equal in magnitude and opposite in the reference frame fixed to movable pulley.

I haven't gone through the complete thread. The easier approach is to calculate distances of masses and pulleys from the ceiling and express the lengths of strings in terms of these distances. I am sorry if this has been already suggested.

 

[arildno]

No, this is not correct. The accelerations are equal in magnitude and opposite in the reference frame fixed to movable pulley.

I haven't gone through the complete thread. The easier approach is to calculate distances of masses and pulleys from the ceiling and express the lengths of strings in terms of these distances. I am sorry if this has been already suggested.

We managed to get there, although I contributed to the confusion of, at various points, using "a_2" both as the relative acceleration and the absolute one.

Furthermore, I managed to just right now remove one of the clearing-up posts, I thought I were editing a new post, rather than an old one..

 

[ehild]

What about a picture, and following Pranav's suggestion, calculating with distances from the ceiling?

There are three equations for the masses, one for the mobile pulley of mass 0 and two equations for the constraints because of the constant length of both strings.

m₄a₄=m₄g-T₁
m₃a₃=m₃g-T₂
m₁a₁=m₁g-T₂

0 a₂ = 2T₂-T₁


a₄+a₂=0
a₁+a₃-2a₂=0

ehild