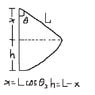gangrene
- 2
- 0
this question has been bugging me for the last few days and my incompetent professor refuses to help me through email.
-----------------------------
Question 10 (1 point)
A child of mass 15.22 kG sitting on a swing whole length is 2.97
meters is pulled up an angle 42.9 degrees and released. The maximum
speed of the child during the subsequent motion (in Meters/sec) is?
Student response 3.98
Correct answer 1.26E0 (1.26 * 10^0 )
Score 0 / 1
-----------------------------
I tried solving this problem by energy conservation and setting max kinetic energy = max potential energy. I figure when the child swings back to equilibrium angle 0, the speed would be greatest with max kinetic energy and with 0 potential energy. The height I used for max potential energy was 2.97-2.97cos42.9 (L-Lcos42.9).
am I doing something wrong?
thx in advance
-----------------------------
Question 10 (1 point)
A child of mass 15.22 kG sitting on a swing whole length is 2.97
meters is pulled up an angle 42.9 degrees and released. The maximum
speed of the child during the subsequent motion (in Meters/sec) is?
Student response 3.98
Correct answer 1.26E0 (1.26 * 10^0 )
Score 0 / 1
-----------------------------
I tried solving this problem by energy conservation and setting max kinetic energy = max potential energy. I figure when the child swings back to equilibrium angle 0, the speed would be greatest with max kinetic energy and with 0 potential energy. The height I used for max potential energy was 2.97-2.97cos42.9 (L-Lcos42.9).
am I doing something wrong?
thx in advance