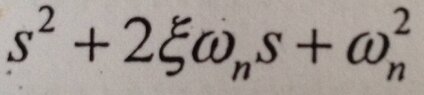fordy2707
- 24
- 0
so I've been tasked with this insane question
obtain the solution of the following quadratic equation
View attachment 5476
how do I solve this, the 'E' (greek letter),is throwing me out,my complete hazardous guess is
2E(S+Wn)2 <--- 2 is a squared sorry my keyboard skills are lacking also 'tut'
any help greatly appreciated
obtain the solution of the following quadratic equation
View attachment 5476
how do I solve this, the 'E' (greek letter),is throwing me out,my complete hazardous guess is
2E(S+Wn)2 <--- 2 is a squared sorry my keyboard skills are lacking also 'tut'
any help greatly appreciated