Solve RC Impulse Response: Voltage @ a RC Circuit

Click For Summary

Discussion Overview

The discussion revolves around the impulse response of an RC circuit, specifically focusing on the voltage across the capacitor (vc(t)). Participants explore theoretical aspects, mathematical approaches, and potential errors in calculations related to the impulse response and the use of Laplace transforms.

Discussion Character

  • Homework-related
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant questions how the voltage can change given that the capacitor's voltage is continuous and initially zero for t < 0.
  • There is a proposal to consider the impulse source as a step function and then differentiate it to find the impulse response.
  • Another participant suggests that the sign of the voltage may be incorrect based on their interpretation of the schematic, indicating a potential misunderstanding of voltage references.
  • Some participants mention the possibility of using Laplace transforms to solve the problem, noting that the transform of the Dirac impulse is simply "1".
  • One participant expresses concern that their university course does not cover Laplace transforms as a method for solving circuits.
  • There is an acknowledgment of a title error in the thread, with clarification that the circuit in question is an RC circuit, not RL.

Areas of Agreement / Disagreement

Participants express uncertainty regarding the sign of the voltage and the approach to finding the impulse response. There is no consensus on the correct interpretation of the voltage references or the appropriateness of using Laplace transforms in this context.

Contextual Notes

Participants note limitations in their course material regarding the use of Laplace transforms, which may affect their problem-solving approaches. There are also unresolved questions about the continuity of voltage across the capacitor during the impulse response.

Frank-95
Messages
51
Reaction score
1
Hello. I would need some clarifications about the impulse response of a RC circuit.

1. Homework Statement

Find the impulse response relative to the vc(t) voltage.

image.jpg


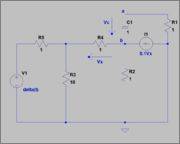
NOTE: delta(t) is the exact dirac's delta of infinite amplitude, not an approximated peak.

Homework Equations



δ(t) = d θ(t) / dt

The Attempt at a Solution



First of all I have a doubt of theoretical nature. If we know that capacitor's voltage is a continuous function (vc(0-) = vc(0+), and know that vc = 0 for t < 0, how can voltage change? Shouldn't it remain 0 for the impulse duration, considering the circuit completely ideal?

Anyway, is it correct to consider the impulse source as a step one, and then derivate the function?

Specifically talking, I found the Thevenin equivalent between a and b, and it comes out:

Rth = 1,6344 Ω
Vth = -0.3313 V

Then I calculate the step response as:

vcθ(t) = -0.3323 θ(t) (1 - e-t/1.6344)

From here is it correct to just derivate this function to get the impulse response?

vcδ(t) = -0.3323/1.6344 e-t/1.6344

Thank you very much.
 
Physics news on Phys.org
That works. Is it possible that you've got the sign wrong? My interpretation of the voltage labeling (arrows) on the schematic would make the node b end of the capacitor the positive reference for the capacitor voltage, and the negative reference for Vx. In other words, Vc = Vb - Va. But the numerical constants look right to me.

You could also solve the problem using Laplace Transforms. The transform of the dirac impulse is simply "1".

Oh, your thread title is misleading: There's no "L" in the circuit, so "RL Impulse Response" doesn't match the problem given.
 
  • Like
Likes   Reactions: Frank-95
That works. Is it possible that you've got the sign wrong?

Yes I probably mistakened the sign.

You could also solve the problem using Laplace Transforms. The transform of the dirac impulse is simply "1".

Unluckily the university course does not consider laplace transform as a way to solve circuits.

Oh, your thread title is misleading: There's no "L" in the circuit, so "RL Impulse Response" doesn't match the problem given.

I apologise. Basically I had written RL, then I noticed the error and wrote RC, but the log in expired and when I refreshed the page there was RL again, but I couldn't change the title once the thread was opened.

Thank you very much.
 
Frank-95 said:
Yes I probably mistakened the sign.
No worries. It happens.
Unluckily the university course does not consider laplace transform as a way to solve circuits.
Wow. Laplace transforms must be one of the most powerful methods for handling differential equations. They're used all the time in circuit analysis. That's a bit of a handicap for you.
I apologise. Basically I had written RL, then I noticed the error and wrote RC, but the log in expired and when I refreshed the page there was RL again, but I couldn't change the title once the thread was opened.
No problem, I can fix it for you.
 

Similar threads

Engineering Signal and Systems: Verify the impulse response of this system
  • · Replies 2 ·
Replies
2
Views
2K
Engineering Impulse Response of an RLC Circuit
  • · Replies 17 ·
Replies
17
Views
6K
Engineering Step response of RC circuit with independent voltage and current sources
  • · Replies 7 ·
Replies
7
Views
3K
Engineering Transient RC Circuit (got answer in s but not in t-domain)
  • · Replies 2 ·
Replies
2
Views
2K
Finding Impulse Response from Block Diagram
  • · Replies 4 ·
Replies
4
Views
4K
Engineering Initial condition of ZSR response of first order circuit:
  • · Replies 1 ·
Replies
1
Views
2K
Impulse response from frequency response
  • · Replies 1 ·
Replies
1
Views
2K
Engineering RC Circuit/Node voltage question
  • · Replies 3 ·
Replies
3
Views
3K
Engineering Solving Impulse Response of RL Circuit
  • · Replies 3 ·
Replies
3
Views
16K
Engineering Circuit theory: capacitor energy storage and discharging/charging times?
  • · Replies 10 ·
Replies
10
Views
3K