Morten1988
- 1
- 0
Hey
I am working on a project about Ray tracing and I find myself stuck on 1 of the 5 questions my teacher has made.
Explain how you can use Fermats principle to solve the formula of reflection and refraction.
I do not now how I am going get from Fermats principle to a formula for reflection and refraction.
I now that Fermats principle is: The path of a ray of light between two points is the path that minimizes the travel time.
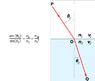
I also know that the formula of refraction is:
Se picture
Now I can't get any father
Hope you can help me out a bit.
Regards
Morten
(sorry about my bad English but I am not native)
I am working on a project about Ray tracing and I find myself stuck on 1 of the 5 questions my teacher has made.
Homework Statement
Explain how you can use Fermats principle to solve the formula of reflection and refraction.
Homework Equations
I do not now how I am going get from Fermats principle to a formula for reflection and refraction.
The Attempt at a Solution
I now that Fermats principle is: The path of a ray of light between two points is the path that minimizes the travel time.
I also know that the formula of refraction is:
Se picture
Now I can't get any father
Hope you can help me out a bit.
Regards
Morten
(sorry about my bad English but I am not native)